101
p5
Found by Achim Flammenkamp in August 1994. The name was
suggested by Bill Gosper, noting that the phase shown below
displays the period in binary.

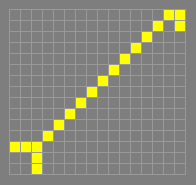
119P4H1V0
c/4 orthogonally, p4
A spaceship discovered by Dean
Hickerson in December 1989, the first spaceship of its kind to be
found. Hickerson then found a small tagalong for this spaceship
which could be attached to one side or both. These three variants of
119P4H1V0 were the only known c/4 orthogonal spaceships until July
1992 when Hartmut Holzwart discovered a larger spaceship, 163P4H1V0.

1-2-3
p3
Found by Dave Buckingham, August 1972. This is one of only
three essentially different p3 oscillators with only three cells in
the rotor. The others are stillater and cuphook.

135-degree MWSS-to-G
The following converter, discovered by
Matthias Merzenich in July 2013. It accepts an MWSS as input, and
produces an output glider travelling at a 135-degree angle relative
to the input direction.

180-degree kickback
The only other two-glider collision besides the
standard kickback that produces a clean output glider with no
leftover ash. The 180-degree change in direction is occasionally
useful in glider synthesis, but is rarely used in signal
circuitry or in self-supporting patterns like the Caterpillar or
Centipede, because 90-degree collisions are generally much easier
to arrange.

(2,1)c/6 spaceship
A knightship that travels obliquely at the
fastest possible speed. To date the only known example of a
spaceship with this velocity is Sir Robin.
(23,5)c/79 Herschel climber
The following glider-supported
Herschel climber reaction used in the self-supporting waterbear
knightship, which can be repeated every 79 ticks, moving the
Herschel 23 cells to the right and 5 cells upward, and releasing
two gliders to the northwest and southwest. As the diagram shows,
it is possible to substitute a loaf or other still lifes for some
or all of the support gliders. This fact is used to advantage at the
front end of the waterbear.
c;79_Herschel_climber.png)
25-cell quadratic growth
A 25-cell quadratic growth pattern found by
Michael Simkin in October 2014, with a bounding box of 21372×172. It
was the smallest-population quadratic growth pattern for two days,
until the discovery of 24-cell quadratic growth. It superseded
wedge, which had held the record for eight years. See
switch-engine ping-pong for the lowest-population
superlinear growth pattern as of July 2018, along with a list of
the record-holders.
25P3H1V0.1
c/3 orthogonally, p3
A spaceship discovered by Dean
Hickerson in August 1989. It was the first c/3 spaceship to be
discovered. In terms of its 25 cells, it is tied with 25P3H1V0.2 as
the smallest c/3 spaceship. Unlike 25P3H1V0.2, it has a population
of 25 in all of its phases, as well as a smaller bounding box.

Martin Grant discovered a glider synthesis for 25P3H1V0.1 on 6
January 2015.
25P3H1V0.2
c/3 orthogonally, p3
A spaceship discovered by David
Bell in early 1992, with a minimum of 25 cells - the lowest number of
cells known for any c/3 spaceship. A note in
Spaceships in Conway's Life indicates that it was found with a
search that limited the number of live cells in each column, and
possibly also the maximum cross-section (4 cells in this case). See
also edge-repair spaceship for a very similar c/3 spaceship with a
minimum population of 26.

In December 2017 a collaborative effort found a 26-glider synthesis
for this spaceship.
26-cell quadratic growth
= wedge.
295P5H1V1
c/5 diagonally, p5
The first spaceship of its type to be
discovered, found by Jason Summers on 22 November 2000.

2c/3 wire
A wire discovered by Dean Hickerson in March 1997, using
his dr search program. It supports signals that travel through
the wire diagonally at two thirds of the speed of light.

Each 2c/3 signal is made up of two half-signals that can be
separated from each other by an arbitrary number of ticks.
Considerable effort has been spent on finding a way to turn a 2c/3
signal 90 or 180 degrees, since this would by one way to prove Life
to be omniperiodic. There is a known 2c/3 converter shown under
signal elbow, which converts a standard 2c/3 signal into a
double-length signal. This is usable in some situations, but
unfortunately it fails when its input is a double-length signal, so
it can't be used to complete a loop.
Noam Elkies discovered a glider synthesis of a reaction that can
repeatably insert a signal into the upper end of a 2c/3 wire. See
stable pseudo-Heisenburp for details. On 11 September 2017, Martin
Grant reduced the input reaction to five gliders, or three gliders
plus a Herschel. With the Herschel option the recovery time is
152 ticks.
See also 5c/9 wire.
2c/7 spaceship
A spaceship travelling at two sevenths of the
speed of light. The only such spaceships that are currently known
travel orthogonally. The first to be found was the weekender,
found by David Eppstein in January 2000. See also
weekender distaff.
2-engine Cordership
The smallest known Cordership, with a minimum
population of 100 cells, discovered by Aidan F. Pierce on 31 December
2017. Luka Okanishi produced a 9-glider synthesis of the spaceship
on the same day.

2-glider collision
Two gliders can react with each other in many
different ways, either at right angles, or else head-on. A large
number of the reactions cleanly destroy both gliders leaving nothing.
Many of the remaining reactions cleanly create some common objects,
and so are used as the first steps in glider synthesis or as part
of constructing interesting objects using rakes. Only a small
number of collisions can be considered dirty due to creating
multiple objects or a mess.
Here is a list of the possible results along with how many
different ways they can occur (ignoring reflections and rotations).
-------------------------------
result right-angle head-on
-------------------------------
nothing 11 17
beehive 1 0
B-heptomino 1 2
bi-block 1 0
blinker 2 1
block 3 3
boat 0 1
eater1 1 0
glider 1 1
honey farm 3 2
interchange 1 0
loaf 0 1
lumps of muck 1 0
octomino 0 1
pi-heptomino 2 1
pond 1 1
teardrop 1 0
traffic light 2 1
four skewed blocks 0 1
dirty 6 0
-------------------------------
The messiest of the two-glider collisions in the "dirty" category is
2-glider mess.
30P5H2V0
2c/5 orthogonally, p5
A spaceship discovered by Paul Tooke
on 7 December 2000. With just 30 cells, it is currently the smallest
known 2c/5 spaceship. A glider synthesis for 30P5H2V0 was found by
Martin Grant in January 2015, based on a predecessor by Tanner
Jacobi.
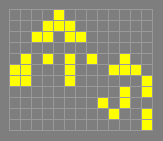
31c/240 Herschel-pair climber
The mechanism defining the rate of
travel of the Centipede and shield bug spaceships. Compare
pi climber. It consists of a pair of Herschels climbing two
parallel chains of blocks. Certain spacings between the block chains
allow gliders from each Herschel to delete the extra ash objects
produced by the other Herschel. Two more gliders escape, one to each
side, leaving only an exact copy of the original block chains, but
shifted forward by 9 cells:

3c/7 spaceship
A spaceship travelling at three sevenths of the
speed of light. The only such spaceships that are currently known
travel orthogonally. The first to be found was the
spaghetti monster, found by Tim Coe in June 2016.
44P5H2V0
2c/5 orthogonally, p5
A spaceship discovered by Dean
Hickerson on 23 July 1991, the first 2c/5 spaceship to be found.
Small tagalongs were found by Robert Wainwright and David Bell that
allowed the creation of arbitrarily large 2c/5 spaceships. These were
the only known 2c/5 spaceships until the discovery of 70P5H2V0 in
December 1992.
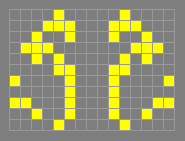
45-degree MWSS-to-G
The following small converter, which accepts an
MWSS or LWSS as input and produces an output glider travelling at a
45-degree angle relative to the input direction.

4 boats
p2

4g-to-5g reaction
A reaction involving 4 gliders which cleanly
produces 5 gliders. The one shown below was found by Dieter Leithner
in July 1992:

The first two gliders collide to produce a traffic light and
glider. The other two gliders react symmetrically with the evolving
traffic light to form four gliders. A glider gun can be built by
using reflectors to turn four of the output gliders so that they
repeat the reaction.
56P6H1V0
c/6 orthogonally, p6
A 56-cell spaceship discovered by
Hartmut Holzwart in 2009, the smallest known c/6 orthogonal spaceship
as of July 2018.

58P5H1V1
c/5 diagonally, p5
A spaceship discovered by Matthias
Merzenich on 5 September 2010. In terms of its minimum population of
58 cells it is the smallest known c/5 diagonal spaceship. It provides
sparks at its trailing edge which can perturb gliders, and this
property was used to create the first c/5 diagonal puffers. These
sparks also allow the attachment of tagalongs which was used to
create the first c/5 diagonal wickstretcher in January 2011.

60P312
p312
Found by Dave Greene, 1 November 2004, based on
92P156.

60P5H2V0
2c/5 orthogonally, p5
A 60-cell spaceship discovered by
Tim Coe in May 1996. It was the first non-c/2 orthogonal spaceship
to be successfully constructed via glider synthesis.

67P5H1V1
c/5 diagonally, p5
A spaceship discovered by Nicolay
Beluchenko in July 2006. It was the smallest known c/5 diagonal
spaceship until the discovery of 58P5H1V1 in September 2010.

70P5H2V0
2c/5 orthogonally, p5
A spaceship discovered by Hartmut
Holzwart on 5 December 1992.

7x9 eater
A high-clearance eater5 variant that can suppress
passing gliders in tight spaces, such as on the inside corner of an
R64 Herschel conduit. Like the eater5 and sidesnagger, the 7×9
eater is able to eat gliders coming from two directions, though this
ability is not commonly used.

86P5H1V1
c/5 diagonally, p5
A spaceship discovered by Jason
Summers on January 8, 2005. It was the smallest known c/5 diagonal
spaceship until the discovery of 67P5H1V1 in July 2006.

92P156
p156
Discovered by Jason Summers on October 31, 2004. It is
actually an eight-barrel glider gun, with all output gliders
suppressed by eater1s. Replacing each pair of eater1s with a
beehive doubles the period and produces 60P312.

Achim's p144
p144) This was found (minus the blocks shown below
on
a cylinder of width 22 by Achim Flammenkamp in July 1994. Dean
Hickerson reduced it to a finite form using figure-8s the same day.
The neater finite form shown here, replacing the figure-8s with
blocks, was found by David Bell in August 1994. See factory for a
use of this oscillator.

Achim's p16
p16
Found by Achim Flammenkamp, July 1994.

Achim's p4
p4
Dave Buckingham found this in a less compact form
(using two halves of sombreros) in 1976. The form shown here was
found by Achim Flammenkamp in 1988. The rotor is two copies of the
rotor of 1-2-3-4, so the oscillator is sometimes called the "dual
1-2-3-4".
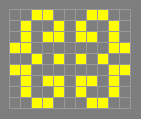
Achim's p8
p8
Found by Achim Flammenkamp, July 1994.

acorn
stabilizes at time 5206
A methuselah found by Charles
Corderman. It has a final population of 633 and covers an area of
215 by 168 cells, not counting the 13 gliders it produces. Its ash
consists of typical stable objects and blinkers, along with the
relatively rare mango and a temporary eater1.

A for all
p6
Found by Dean Hickerson in March 1993.

against the grain
A term used for negative spaceships travelling in
zebra stripes agar, perpendicular to the stripes, and also for
against-the-grain grey ships.
Below is a sample signal, found by Hartmut Holzwart in April
2006, that travels against the grain at 2c/3. This "negative
spaceship" travels upward and will quickly reach the edge of the
finite patch of stabilized agar shown here.

Holzwart proved in 2006 that 2c/3 is the maximum speed at which
signals can move non-destructively against the grain through zebra
stripes agar.
against-the-grain grey ship
A grey ship in which the region of
density 1/2 consists of lines of ON cells lying perpendicular to the
direction in which the spaceship moves. See also
with-the-grain grey ship.
agar
Any pattern covering the whole plane that is periodic in both
space and time. The simplest (nonempty) agar is the stable one
extended by the known spacefillers. For some more examples see
chicken wire, houndstooth agar, onion rings, squaredance and
Venetian blinds. Tiling the plane with the pattern O......O
produces another interesting example: a p6 agar which has a phase of
density 3/4, which is the highest yet obtained for any phase of an
oscillating pattern. See lone dot agar for an agar composed of
isolated cells.
aircraft carrier
p1
This is the smallest still life that has more
than one island.

airforce
p7
Found by Dave Buckingham in 1972. The rotor consists
of two copies of that used in the burloaferimeter.

AK47 reaction
The following reaction (found by Rich Schroeppel and
Dave Buckingham) in which a honey farm predecessor, catalysed by an
eater and a block, reappears at another location 47 generations
later, having produced a glider and a traffic light. This was in
1990 the basis for the Dean Hickerson's construction of the first
true p94 gun, and for a very small (but pseudo) p94 glider gun
found by Paul Callahan in July 1994. (The original true p94 gun was
enormous, and has now been superseded by comparatively small
Herschel loop guns and Mike Playle's tiny AK94 gun.)

AK94 gun
The smallest known gun using the AK47 reaction, found by
Mike Playle in May 2013 using his Bellman program.

almost knightship
A promising partial result discovered by Eugene
Langvagen in March 2004. This was an early near miss in the ongoing
search for a small elementary (2,1)c/6 knightship. After six
generations, only two cells are incorrect.

almosymmetric
p2
Found in 1971.

anteater
A pattern that consumes ants. Matthias Merzenich
discovered a c/5 anteater on 15 April 2011. See wavestretcher for
details.
ants
p5 wick
The standard form is shown below. It is also possible
for any ant to be displaced by one or two cells relative to either or
both of its neighbouring ants. Dean Hickerson found fenceposts for
both ends of this wick in October 1992 and February 1993. See
electric fence, and also wickstretcher.

apgsearch
One of several versions of a client-side Ash Pattern
Generator soup search script by Adam P. Goucher, for use with
Conway's Life and a wide variety of other rules. Development of the
original Golly-based Python script started in August 2014. After
the addition in 2016 of apgnano (native C++) and apgmera
(self-modifying, 256-bit SIMD compatibility), development continues
in 2017 with apgluxe (Larger Than Life and Generations rules, more
soup shapes). Several customized variants of the Python script have
also been created by other programmers, to perform types of searches
not supported by Goucher's original apgsearch 1.×.
All of these versions of the search utility work with a "haul" that
usually consists of many thousands or millions of random soup
patterns. Each soup is run to stability, and detailed object
census results are reported to Catagolue. For any rare objects
discovered in the ash, the source soup can be easily retrieved from
the Catagolue server.
APPS
c/5 orthogonally, p30
An asymmetric PPS. The same as the
SPPS, but with the two halves 15 generations out of phase with one
another. Found by Alan Hensel in May 1998.
ark
A pair of mutually stabilizing switch engines. The archetype
is Noah's ark. The diagram below shows an ark found by Nick Gotts
that takes until generation 736692 to stabilize, and can therefore be
considered as a methuselah.

arm
A long extension, sometimes also called a "wing", hanging off
from the main body of a spaceship or puffer perpendicular to the
direction of travel. For example, here is a sparking c/3 spaceship
which contains two arms.

Many known spaceships have multiple arms, usually fairly narrow.
This is an artefact of the search methods used to find such
spaceships, rather than an indication of what a "typical" spaceship
might look like.
For an alternate meaning see construction arm.
armless
A method of generating slow salvos across a wide range of
lanes without using a construction arm with a movable elbow.
Instead, streams of gliders on two fixed opposing lanes collide
with each other to produce clean 90-degree output gliders. Slowing
down one of the streams by 8N ticks will move the output lanes of the
gliders toward the source of that stream by N full diagonals. This
construction method was used to create the supporting slow salvos in
the half-baked knightships, and also in the Parallel HBK gun.
ash
The stable or oscillating objects left behind when a chaotic
reaction stabilizes, or "burns out". Experiments show that for random
soups with moderate initial densities (say 0.25 to 0.5) the
resulting ash has a density of about 0.0287. (This is, of course,
based on what happens in finite fields. In infinite fields the
situation may conceivably be different in the long run because of the
effect of certain initially very rare objects such as replicators.)
asynchronous
Indicates that precise relative timing is not needed for
two or more input signals entering a circuit, or two or more sets
of gliders participating in a glider synthesis. In some cases
the signals or sets of gliders can arrive in any order at all - i.e.,
they have non-overlapping effects.
However, in some cases such as slow salvo constructions, there is
a required order for some of the incoming signals. These signals can
still be referred to as "asynchronous" because the number of ticks
between them is infinitely adjustable: arbitrarily long delays can
be added with no change to the final result. Compare synchronized.
aVerage
p5
Found by Dave Buckingham, 1973. The average number of
live rotor cells is five (V), which is also the period.

B29
c/4 diagonally, p4
The following spaceship, found by Hartmut
Holzwart in April 2004. A glider synthesis of this spaceship was
completed by Tanner Jacobi in April 2015.

B-52 bomber
The following p104 double-barrelled glider gun. It
uses a B-heptomino and emits one glider every 52 generations. It
was found by Noam Elkies in March 1996, except that Elkies used
blockers instead of molds, the improvement being found by David
Bell later the same month.

B60
A Herschel conduit discovered by Michael Simkin in 2015 using
his search program, CatForce. It is one of two known Blockic
elementary conduits. After 60 ticks, it produces a Herschel
rotated 180 degrees at (-6,-10) relative to the input. It can most
easily be connected to another B60 conduit, producing a closed loop,
the Simkin glider gun.
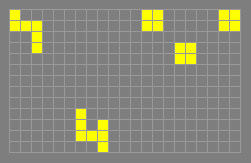
babbling brook
Any oscillator whose rotor consists of a string of
cells each of which is adjacent to exactly two other rotor cells,
except for the endpoints which are adjacent to only one other rotor
cell. Compare muttering moat. Examples include the beacon, the
great on-off, the light bulb and the spark coil. The following
less trivial example (by Dean Hickerson, August 1997) is the only one
known with more than four cells in its rotor. It is p4 and has a
6-cell rotor.

backrake
Another term for a backwards rake. A p8 example by Jason
Summers is shown below. See total aperiodic for a p12 example.

backward glider
A glider which moves at least partly in the
opposite direction to the puffer(s) or spaceship(s) under
consideration.
bait
An object in a converter, usually a small still life, that
is temporarily destroyed by an incoming signal, but in such a way
that a usable output signal is produced. In general such a converter
produces multiple output signals (or a signal splitter is added)
and one branch of the output is routed to a factory mechanism that
rebuilds the bait object so that the converter can be re-used.
baker
c p4 fuse
A fuse by Keith McClelland.

baker's dozen
p12
A loaf hassled by two blocks and two
caterers. The original form (using p4 and p6 oscillators to do the
hassling) was found by Robert Wainwright in August 1989.

bakery
p1
A common formation of two bi-loaves.

barberpole
Any p2 oscillator in the infinite sequence bipole,
tripole, quadpole, pentapole, hexapole, heptapole ... (It
wasn't my idea to suddenly change from Latin to Greek.) This sequence
of oscillators was found by the MIT group in 1970. The term is also
used (usually in the form "barber pole") to describe other
extensible sections of oscillators or spaceships, especially those
(usually of period 2) in which all generations look alike except for
a translation and/or rotation/reflection. Any barberpole can be
lengthened by the reaction shown in barbershop. See also
pseudo-barberpole.
barberpole intersection
= quad
barbershop
An object created by Jason Summers in 1999 which builds an
infinite barberpole. It uses slide guns to repeatedly lengthen a
barberpole at a speed of c/124. The key lengthening reaction from
Mark Niemiec is shown below:

barge
p1

beacon
p2
The third most common oscillator. Found by Conway,
March 1970.

beacon maker
c p8 fuse
beehive and dock
p1

beehive stopper
A Spartan logic circuit discovered by Tanner
Jacobi on 12 May 2015. It converts an input glider signal into a
beehive, in such a way that the beehive can cleanly absorb a single
glider from a perpendicular glider stream. The circuit can't be
re-used until the beehive "bit" is cleared by the passage of at least
one perpendicular input.
This term has sometimes been used for the beehive catalyst
variant of SW-2, and also for Paul Callahan's larger
glider stopper, which also provides optional 0-degree and
180-degree glider outputs.
beehive with tail
p1

Bellman
A program for searching catalytic reactions, developed by
Mike Playle, which successfully found the Snark.
Beluchenko's p37
p37
Found by Nicolay Beluchenko on April 14, 2009.
It was the first period 37 oscillator to be found, and remains
the smallest.

Beluchenko's p51
p51
Found by Nicolay Beluchenko on February 17,
2009. It was the first non-trivial period 51 oscillator to be
found.

BFx59H
One of the earliest and most remarkable converters,
discovered by Dave Buckingham in July 1996. In 59 generations it
transforms a B-heptomino into a clean Herschel with very good
clearance, allowing easy connections to other conduits. It forms the
final stage of many of the known composite conduits, including the
majority of the original sixteen Herschel conduits. Here a
ghost Herschel marks the output location:

B-heptomino
stabilizes at time 148
This is a very common
methuselah that evolves into three blocks, two gliders and a
ship after 148 generations. Compare with Herschel, which appears
at generation 20 of the B-heptomino's evolution. B-heptominoes
acquired particular importance in 1996 due to Dave Buckingham's work
on B tracks. See in particular
My Experience with B-heptominos in Oscillators.

This pattern often arises with the cell at top left shifted one
space to the left, producing a seven-bit polyplet that shares the
same eight-bit descendant but is not technically a heptomino at all.
This alternate form is shown as the input for elementary
converter patterns such as BFx59H and BRx46B. This is standard
practice for elementary conduits, since many of these conduits do
in fact produce this alternate form as output.
The B-heptomino is considered a failed puffer or failed
spaceship, since on its own it travels at c/2 for only a short time
before being affected by its own trailing debris. However, it can be
stabilized into a c/2 puffer or into a clean c/2 rake or spaceship.
See, e.g., ecologist.
bi-block puffer
Any puffer whose output is bi-blocks. The term
is particularly used for p8 c/2 puffers, in which case a
bi-block fuse is created. A bi-block puffer is easily made using
two backrakes whose gliders impact symmetrically. Jason Summers
welded two backrakes to form a more compact puffer, as shown below.

By periodically burning the bi-block fuse using perturbations by a
following backrake and spaceships, c/2 rakes can be created for all
periods that are a multiple of eight.
big glider
c/4 diagonally, p4
This was found by Dean Hickerson in
December 1989 and was the first known diagonal spaceship other than
the glider.

big S
p1

bi-loaf
This term has been used in at least three different senses. A
bi-loaf can be half a bakery:
.png)
or it can be the following much less common still life:
.png)
or the following pure glider generator:
.png)
bi-pond
p1

bistable switch
A Spartan memory cell found by Paul Callahan in
1994. It can be in one of two states, containing either a boat or
a block. Input gliders on the appropriate paths can change the boat
to a block, or vice-versa, while also emitting an output glider.
Unlike many memory cells, attempts to change the state to the one it
is already in are ignored with the glider passing through with no
reaction. This makes it easy to reset the memory cell to a known
state. Which of the two states is considered the SET and which
considered the RESET is just a matter of convention.
The pattern below shows the "boat" state of the memory cell in its
original 1994 form. Two gliders are also shown to indicate the input
paths used to change the states. A smaller version is shown under
century eater, with the circuit in its "block" state.
As shown, the rightmost glider changes the state from a boat to a
block and emits a glider to the upper right, while the leftmost
glider passes through unchanged. Alternatively, when the state
contains a block, then the leftmost glider changes the state from a
block to a boat, and emits a glider to the lower right, while the
rightmost glider passes through unchanged.

bit
A live cell, if used in reference to still life population.
For example, a beehive is a 6-bit still life. Other uses generally
involve information storage: a memory cell such as a honey bit
that can hold one binary bit of information for later retrieval.
biting off more than they can chew
p3
Found by Peter Raynham, July
1972.

blasting cap
after the shape at generation 1
. A
term used at MIT and still occasionally encountered.
blinker
p2
The smallest and most common oscillator. Found by
Conway, March 1970.

blinker fuse
A clean fuse made from a row of blinkers separated
by one cell gaps. The blinker row wick is usually created by a
blinker puffer. The fuse can burn in at least three different
ways at a speed of 2c/3 depending on the method used to ignite the
end of the row of blinkers. This variant has found the most use. The
burning advances 12 cells every 18 generations.

Fuses can also be made with blinker rows which contain occasional two
cell gaps, since the burning reaction is able to bridge those gaps.
blinker puffer
Any puffer whose output is blinkers. However, the
term is particularly used for p8 c/2 puffers. The first such blinker
puffer was found by Robert Wainwright in 1984, and was unexpectedly
simple:
.png)
Since then many more blinker puffers have been found. The following
one was found by David Bell in 1992 when he was trying to extend an
x66:
.png)
The importance of this larger blinker puffer (and others like it), is
that the engine which produces the blinker output is only p4. The
blinker row produced by the puffer can easily be ignited, and the
resulting blinker fuse burns cleanly with a speed of 2c/3. When
the burning catches up to the engine, it causes a phase change in
the puffer. This fact allows p8 blinker puffers to be used to
construct rakes of all periods which are large multiples of four.
blinker pull
The following glider/blinker collision, which moves a
blinker (-1,3) toward the glider source:

blinkers bit pole
p2
Found by Robert Wainwright, June 1977.

blinker ship
A growing spaceship in which the wick consists of a
line of blinkers. An example by Paul Schick based on his
Schick engine is shown below. Here the front part is p12 and moves
at c/2, while the back part is p26 and moves at 6c/13. Every 156
generations 13 blinkers are created and 12 are destroyed, so the wick
becomes one blinker longer.

blockade
p1
A common formation of four blocks. The final form of
lumps of muck.

block and dock
p1

block and glider
stabilizes at time 106

blocker
p8
Found by Robert Wainwright. See also filter.

block on table
p1

block pull
The following glider/block collision, which moves a block
(2,1) toward the glider source. Performing this reaction twice using
a salvo of two gliders can move a block diagonally back by three
cells, which can be of use for a sliding block memory.

block pusher
A pattern emitting streams of gliders which can
repeatedly push a block further away. This can be used as part of a
sliding block memory.
The following pattern, in which three gliders push a block one cell
diagonally, is an example of how a block pusher works.
A universal construction elbow recipe library is also likely to
contain one or more block-pushing reactions, since blocks are
commonly used as elbows.
blom
stabilizes at time 23314
The following methuselah, found by
Dean Hickerson in July 2002.
blonk
A block or a blinker. This term is mainly used in the
context of sparse Life and was coined by Rich Schroeppel in
September 1992.
blonker
p6
The following oscillator, found by Nicolay Beluchenko
in April 2004.

boat-bit
A binary digit represented by the presence of a boat next
to a snake (or other suitable object, such as an
aircraft carrier). The bit can be toggled by a glider travelling
along a certain path. A correctly timed glider on a crossing path
can detect whether the transition was from 1 to 0 (in which case the
crossing glider is deleted) or from 0 to 1 (in which case it passes
unharmed). Three gliders therefore suffice for a
non-destructive read. The mechanisms involved are shown in the
diagram below. Here the bit is shown in state 0. It is about to be
set to 1 and then switched back to 0 again. The first crossing
glider will survive, but the second will be destroyed.
.png)
In January 1997 David Bell found a method of reading the bit while
setting it to 0. A MWSS is fired at the boat-bit. If it is
already 0 (absent) then the MWSS passes unharmed, but if it is 1
(present) then the boat and the MWSS are destroyed and, with the help
of an eater1, converted into a glider which travels back along
exactly the same path that is used by the gliders that toggle the
boat-bit.
.png)
There are many other equivalent methods based on alternate incoming
test signals.
boat maker
c p4 fuse

boat-tie
p1
A 10-cell still life consisting of two boats placed
tip-to-tip. The name is a pun on "bow tie".

boojum reflector
p1
Dave Greene's name for the following 180-degree
glider reflector which he found in April 2001, winning $100
bounties offered by Alan Hensel and Dieter Leithner. The name is
taken from Lewis Carroll's _The Hunting of the Snark_, referring to
the fact that a small 90-degree stable reflector was really what was
wanted. 180-degree reflectors are relatively undesirable and have
limited use in larger circuitry constructions.
The boojum reflector was the smallest and fastest known stable
reflector until the discovery of the rectifier in 2009, followed by
the Snark in 2013.

bookends
p1

boss
p4
Found by Dave Buckingham, 1972.

bottle
p8
Found by Achim Flammenkamp in August 1994. The name is a
back-formation from ship in a bottle.

bounding box
The smallest rectangular array of cells that contains
the whole of a given pattern. For oscillators and guns this
usually is meant to include all phases of the pattern, but in the
case of guns, the outgoing stream(s) are excluded. The bounding box
is one of the standard ways to measure the size of an object; the
other standard metric is the population.
brain
c/3 orthogonally, p3
Found by David Bell, May 1992.

branching spaceship
An extensible spaceship containing components
which can be attached in multiple ways so that the result can contain
arbitrarily many arms arranged like a binary tree. Here is an
example of a period 2 c/2 branching spaceship, which also includes a
wicktrailer:

Branching spaceships have also been constructed for other speeds,
such as c/3.
breeder
Any pattern whose population grows at a quadratic rate,
although it is usual to exclude spacefillers. It is easy to see
that this is the fastest possible growth rate.
The term is also sometimes used to mean specifically the breeder
created by Bill Gosper's group at MIT, which was the first known
pattern exhibiting superlinear growth.
There are four common types of breeder, known as MMM, MMS, MSM and
SMM (where M=moving and S=stationary). Typically an MMM breeder is a
rake puffer, an MMS breeder is a puffer producing puffers which
produce stationary objects (still lifes and/or oscillators), an
MSM breeder is a gun puffer and an SMM breeder is a rake gun. There
are, however, less obvious variants of these types. Other less
common breeder categories (SSS, hybrid MSS/MSM, etc.) can be created
with some difficulty, based on universal constructor technology;
see Pianola breeder.
The original breeder was of type MSM (a p64 puffer puffing p30
glider guns). The known breeder with the smallest initial population
is switch-engine ping-pong.
broken lines
A pattern constructed by Dean Hickerson in May 2005
which produces complex broken lines of gliders and blocks.
BRx46B
A Spartan elementary conduit discovered by Michael Simkin
on 25 April 2016, one of the relatively few known conduits that can
move a B-heptomino input to a B-heptomino output without an
intervening Herschel stage.
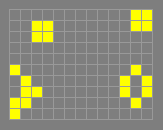
buckaroo
p30
A queen bee shuttle stabilized at one end by an
eater in such a way that it can turn a glider, as shown below. The
glider turning reaction uses a banana spark and is
colour-preserving. The mechanism was found by Dave Buckingham in
the 1970s. The name is due to Bill Gosper.

bunnies
stabilizes at time 17332
This is a parent of rabbits
and was found independently by Robert Wainwright and Andrew
Trevorrow.

burloaferimeter
p7
Found by Dave Buckingham in 1972. See also
airforce.

burn
A reaction which travels indefinitely as a wave through the
components of a wick or an agar. A burning wick is known as a
fuse.
If the object being burned has a spatial periodicity, then the
active area of the burning usually remains bounded and so eventually
develops a periodicity too. It is unknown whether this will always
occur.
The speed of burning can range from arbitrarily slow up to the
speed of light. The results of burning can be clean (leaving no
debris), or leaving debris usually much different from the original
object. In rare cases, a reburnable fuse produces an exact copy of
the original object, allowing the creation of objects such as the
telegraph.
In many useful cases burning can be initiated by impacting an
object with gliders or other spaceships. An object might be able
to burn in more than one way, depending on how the burn is initiated.
butterfly
The following pattern, or the formation of two beehives
that it evolves into after 33 generations. (Compare teardrop,
where the beehives are five cells closer together.)

by flops
p2
Found by Robert Wainwright.

c/10 spaceship
A spaceship travelling at one tenth of the
speed of light. The first such spaceship to be discovered was the
orthogonally travelling copperhead, found by 'zdr' on 5 March 2016.
Simon Ekström found the related fireship two weeks later. A
Caterloopillar can theoretically be configured to move at c/10, but
there are technical difficulties with speeds of the form 4n+2, and as
of June 2018 this has not been done in practice.
c/2 spaceship
A spaceship travelling at half the speed of light.
Such spaceships necessarily move orthogonally. The first to be
discovered was the LWSS. For other examples see Coe ship,
ecologist, flotilla, hammerhead, hivenudger, HWSS, MWSS,
puffer train, puff suppressor, pushalong, Schick engine,
sidecar, still life tagalong and x66.
c/4 spaceship
A spaceship travelling at one quarter of the
speed of light. The first such spaceship to be discovered was, of
course, the glider, and this remained the only known example until
December 1989, when Dean Hickerson found the first orthogonal
example, 119P4H1V0, and also a new diagonal example (the
big glider). For other examples see B29, Canada goose, crane,
Enterprise, edge-repair spaceship (third pattern),
non-monotonic, Orion, quarter, sparky, swan and tagalong.
It is known that c/4 is the fastest possible speed for a (45-degree)
diagonal spaceship.
c/6 spaceship
A spaceship travelling at one sixth of the
speed of light. The first such spaceship to be discovered was the
dragon, found by Paul Tooke in April 2000. The first diagonally
moving example was the seal, found by Nicolay Beluchenko in
September 2005. Another orthogonal c/6 spaceship, found by Paul
Tooke in March 2006, is shown below. For the smallest known c/6
spaceship see 56P6H1V0.

A Caterloopillar can theoretically be configured to move at c/6,
but there are technical difficulties with speeds of the form 4n+2,
and as of July 2018 this has not been done in practice.
c/7 spaceship
A spaceship travelling at one seventh of the
speed of light. The first such spaceship to be discovered was the
diagonally travelling lobster, found by Matthias Merzenich in
August 2011. The first known orthogonal c/7 spaceship was the
loafer, discovered by Josh Ball in February 2013. A
Caterloopillar has been configured to move at c/7.
caber tosser
t
for some constant c, and which contains a glider (or other
spaceship) bouncing between a slower receding spaceship and a fixed
reflector which emits a spaceship (in addition to the reflected
one) whenever the bouncing spaceship hits it.
As the receding spaceship gets further away the bouncing spaceship
takes longer to complete each cycle, and so the extra spaceships
emitted by the reflector are produced at increasingly large
intervals. More precisely, if v is the speed of the bouncing
spaceship and u the speed of the receding spaceship, then each
interval is (v+u)/(v-u) times as long as the previous one. The
population at time t is therefore n.log(t)/log((v+u)/(v-u)) + O(1),
where n is the population of one of the extra spaceships (assumed
constant).
The first caber tosser was built by Dean Hickerson in May 1991.
Callahan G-to-H
A stable glider reflector and glider-to-Herschel
converter discovered by Paul Callahan in November 1998. Its
recovery time is 575 ticks. The initial stage converts two gliders
into a Herschel. A ghost Herschel in the pattern below marks the
output location:

The glider from the southeast can be supplied by an Fx77 + L112
+ Fx77 Herschel track, or by reflecting the output Herschel's FNG
as in the p8 G-to-H. See also Silver reflector, Silver G-to-H.
Cambridge pulsar CP 48-56-72
= pulsar (The numbers refer to the
populations of the three phases. The Life pulsar was indeed
discovered at Cambridge, like the first real pulsar a few years
earlier.)
Canada goose
c/4 diagonally, p4
Found by Jason Summers, January
1999. It consists of a glider plus a tagalong.

At the time of its discovery the Canada goose was the smallest known
diagonal spaceship other than the glider, but this record has since
been beaten, first by the second spaceship shown under Orion, and
more recently by quarter.
candelabra
p3
By Charles Trawick. See also the note under cap.

candlefrobra
p3
Found by Robert Wainwright in November 1984.
.png)
The following diagram shows that a pair of these can act in some ways
like killer toads. See also snacker.
.png)
canoe
p1

cap
The following induction coil. It can also easily be stabilized
to form a p3 oscillator. See candelabra for a slight variation on
this.

carnival shuttle
p12
Found by Robert Wainwright in September 1984
(using MW emulators at the end, instead of the monograms shown
here).
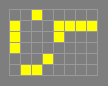
catacryst
A 58-cell quadratic growth pattern found by Nick Gotts in
April 2000. This was formerly the smallest such pattern known, but
has since been superseded by the related metacatacryst. See
switch-engine ping-pong for the lowest-population
superlinear growth pattern as of July 2018, along with a list of
the record-holders.
The catacryst consists of three arks plus a glider-producing
switch engine. It produces a block-laying switch engine every
47616 generations. Each block-laying switch engine has only a finite
life, but the length of this life increases linearly with each new
switch engine, so that the pattern overall grows quadratically, as an
unusual type of MMS breeder.
Catagolue
An online database of objects in Conway's Game of Life and
similar cellular automata, set up by Adam P. Goucher in 2015 at
http://catagolue.appspot.com. It gathers data from a distributed
search of random initial configurations and records the eventual
decay products. Within a year of operation it had completed a
census of the ash objects from over two trillion asymmetric 16×16
soups. As of June 2018, well over two hundred trillion ash objects
have been counted, from over a trillion asymmetric soups.
It is often possible to use Catagolue search results find
equivalent glider synthesis recipes for selected parts of
long-running active reactions. These random soup searches have
made it possible to find efficient construction methods for thousands
of increasingly rare still lifes and oscillators, and the
occasional puffer or spaceship. In many of these cases a
glider synthesis was previously very difficult or unknown.
catalyst
An object that participates in a reaction but emerges from
it unharmed. All eaters are catalysts. Some small still lifes
can act as catalysts in some situations, such as the block, ship,
and tub. The still lifes and oscillators that form a conduit are
examples of catalysts.
A relatively rare form of catalysis occurs in a
transparent debris effect, where the catalyst in question is
completely destroyed and then rebuilt. The term is also sometimes
used for a modification of an active reaction in a rake by passing
spaceships.
catch and throw
A technology used (e.g., in the Caterpillar) to
adjust the timing of a glider by turning it into a stationary object
using one interaction, and then later restoring it using a second
interaction. The interactions are caused by passing objects which
are not otherwise affected. The direction of the glider is not
usually changed.
Here is an example where a glider is turned into a boat by the
first LWSS, and is then restored by the remaining spaceships:

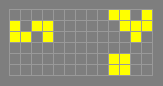
caterer
p3
Found by Dean Hickerson, August 1989. Compare with
jam. In terms of its minimum population of 12 this is the
smallest p3 oscillator. See also double caterer and
triple caterer.
More generally, any oscillator which serves up a bit in the same
manner may be referred to as a caterer.
Caterloopillar
A family of adjustable-speed spaceships constructed
by Michael Simkin in 2016, based on an "engineless caterpillar" idea
originally proposed by David Bell. The front and back halves of
Caterloopillars each function as universal constructors, with each
half constructing the building blocks of the other half, while also
reading and moving a construction tape. The overall design is
reminiscent of M.C. Escher's lithograph "Drawing Hands". The name
"Caterloopillar" is a reference to Douglas Hofstader's Strange Loop
concept.
Simkin has written an automated script that can construct a
Caterloopillar for any rational speed strictly less than c/4, with
some exceptions. Speeds closer to the c/4 limit in general require
larger constructions, and for any given computer system it is easy to
choose a speed that makes it impractical to construct a
Caterloopillar.
As of June 2018 one significant remaining exception is that
Caterloopillars with periods c/(6+4N) can't be constructed. This is
only a limitation of the current construction script, not of the
underlying Caterloopillar toolkit. For technical reasons, the
lowest speed that the current script can produce is around c/95. The
slowest Caterloopillars that have been explicitly constructed to date
are c/87 and c/92. These are among the smallest in terms of
population, though their bounding boxes are larger than some of the
higher-speed Caterloopillars.
Caterpillar
A spaceship that works by laying tracks at its front
end. The first example constructed was a p270 17c/45 spaceship built
by Gabriel Nivasch in December 2004, based on work by himself, Jason
Summers and David Bell. This Caterpillar has a population of about
12 million in each generation and was put together by a computer
program that Nivasch wrote. At the time it was by far the largest
and most complex Life object ever constructed, and it is still one of
the largest in terms of population.
The 17c/45 Caterpillar is based on the following reaction between a
pi-heptomino and a blinker:
.png)
In this reaction, the pi moves forward 17 cells in the course of 45
generations, while the blinker moves back 6 cells and is rephased.
This reaction has been known for many years, but it was only in
September 2002 that David Bell suggested that it could be used to
build a 17c/45 spaceship, based on a reaction he had found in which
pi-heptominoes crawling along two rows of blinkers interact to emit a
glider every 45 generations. Similar glider-emitting interactions
were later found by Gabriel Nivasch and Jason Summers. The basic
idea of the spaceship design is that streams of gliders created in
this way can be used to construct fleets of standard spaceships
which convey gliders to the front of the blinker tracks, where they
can be used to build more blinkers.
A different Caterpillar may be possible based on the following
reaction, in which the pattern at top left reappears after 31
generations displaced by (13,1), having produced a new NW-travelling
glider. In this case the tracks would be waves of backward-moving
gliders.
.png)
For other Caterpillar-type constructions see Centipede,
waterbear, half-baked knightship, and Caterloopillar.
CatForce
An optimized search program written by Michael Simkin in
2015, using brute-force enumeration of small Spartan objects in a
limited area, instead of a depth-first tree search. One major
purpose of CatForce is to find glider-constructible completions for
signal conduits. An early CatForce discovery was the B60 conduit,
which enabled a record-breaking new glider gun.
cauldron
p8
Found in 1971 independently by Don Woods and Robert
Wainwright. Compare with Hertz oscillator.

CC semi-Snark
A small 90-degree colour-changing glider reflector
requiring two input gliders on the same lane for each output glider.
It was discovered by Sergei Petrov on 1 July 2013, using a
custom-written search utility. It functions as a very compact
period doubler in some signal circuitry, for example the
linear propagator. The semi-Snark can period-double a regular
glider stream of period 51 or more, or an intermittent stream
with two gliders every 67 ticks or more, since the block reset glider
can be sent just 16 ticks before its partner.

cell
The fundamental unit of space in the Life universe. The term is
often used to mean a live cell - the sense is usually clear from the
context.
cellular automaton
A certain class of mathematical objects of which
Life is an example. A cellular automaton consists of a number of
things. First there is a positive integer n which is the dimension
of the cellular automaton. Then there is a finite set of states S,
with at least two members. A state for the whole cellular automaton
is obtained by assigning an element of S to each point of the
n-dimensional lattice Zn (where Z is the set of all integers). The
points of Zn are usually called cells. The cellular automaton also
has the concept of a neighbourhood. The neighbourhood N of the
origin is some finite (nonempty) subset of Zn. The neighbourhood of
any other cell is obtained in the obvious way by translating that of
the origin. Finally there is a transition rule, which is a function
from SN to S (that is to say, for each possible state of the
neighbourhood the transition rule specifies some cell state). The
state of the cellular automaton evolves in discrete time, with the
state of each cell at time t+1 being determined by the state of its
neighbourhood at time t, in accordance with the transition rule.
There are some variations on the above definition. It is common to
require that there be a quiescent state, that is, a state such that
if the whole universe is in that state at generation 0 then it will
remain so in generation 1. (In Life the OFF state is quiescent, but
the ON state is not.) Other variations allow spaces other than Zn,
neighbourhoods that vary over space and/or time, probabilistic or
other non-deterministic transition rules, etc.
It is common for the neighbourhood of a cell to be the 3×...×3
(hyper)cube centred on that cell. (This includes those cases where
the neighbourhood might more naturally be thought of as a proper
subset of this cube.) This is known as the Moore neighbourhood.
Centipede
31c/240 orthogonally, p240
The smallest known 31c/240
spaceship, constructed by Chris Cain in September 2014 as a
refinement of the shield bug.
century
stabilizes at time 103
This is a common pattern which
evolves into three blocks and a blinker. In June 1996 Dave
Buckingham built a neat p246 gun using a century as the engine.
See also bookend and diuresis.

century eater
A 20-cell still life that functions as an eater for
the active reaction produced by any century relative. The most
well-known use is to replace a four-object constellation in Paul
Callahan's bistable switch, as shown below. In September 2014 Josh
Ball showed that a variant of this still life has a relatively
inexpensive slow glider construction recipe.

At T=256 the active reaction produces an eight-cell pattern sharing
the same grandchild as a century. The century eater at the top of
the pattern catalyzes this pattern produce a clean spark.
channel
A lane or signal path used in construction circuitry.
Until the invention of single-channel construction arms, signals
in a channel would usually be synchronized with one or more
coordinated signals on other paths, as in the Gemini, which used
twelve channels to run three construction arms simultaneously, or the
10hd Demonoid which needed only two channels. See also Geminoid.
chaotic growth
An object whose fate is unknown, except that it
appears to grow forever in an unpredictable manner. In Life, no
pattern has yet been found that is chaotic. This is in contrast to
many other Life-like rules, where even small objects can appear to
grow chaotically.
It is possible that chaotic growth may occur rarely or even
regularly for large enough random Life objects, but if so the minimum
size of such patterns must be larger than what can currently be
experimentally simulated (but see novelty generator).
In any case, it is not decidable whether a pattern that apparently
grows randomly forever is in fact displaying chaotic growth.
Continuing to evolve such a pattern might at any time result in it
suddenly cleaning itself up and becoming predictable.
chemist
p5

C-heptomino
Name given by Conway to the following heptomino, a less
common variant of the B-heptomino.

Cheshire cat
A block predecessor by C. R. Tompkins that
unaccountably appeared both in Scientific American and in
Winning Ways. See also grin.

chicken wire
A type of stable agar of density 1/2. The
simplest version is formed from the tile:
.png)
But the "wires" can have length greater than two and need not all be
the same. For example:
.png)
chirality
A term borrowed from chemistry to describe asymmetrical
patterns with two distinct mirror-image orientations. One common use
is in relation to Herschel transmitters, where the spacing between
the two gliders in the tandem glider output can limit the
receiver to a single chirality.
cis-beacon on anvil
p2

cis-beacon on table
p2

cis-boat with tail
p1

cis-mirrored R-bee
p1

clean
Opposite of dirty. A reaction which produces a small number
of different products which are desired or which are easily deleted
is said to be clean. For example, a puffer which produces just one
object per period is clean. Clean reactions are useful because they
can be used as building blocks in larger constructions.
When a fuse is said to be clean, or to burn cleanly, this
usually means that no debris at all is left behind.
clearance
In signal circuitry, the distance from an edge shooter
output lane to the last unobstructed lane adjacent to the
edge-shooter circuitry. For example, an Fx119 inserter has an
unusually high 27hd clearance.
Also, oscillator and eater variants may be said to have better
clearance if they allow gliders or other signals to pass closer
to them than the standard variant allows. The following
high-clearance eater1 variant by Karel Suhajda allows gliders to
pass one lane closer on the southeast side, than is allowed by the
standard fishhook shape.

This is considered to be a variant of the eater1 because the
reaction's rotor is exactly the same, even though three cells in
this variant are too overpopulated to allow a birth, instead of
underpopulated as in a standard eater1 glider-eating reaction.
clock
p2
Found by Simon Norton, May 1970. This is the fifth or
sixth most common oscillator, being about as frequent as the
pentadecathlon, but much less frequent than the blinker, toad,
beacon or pulsar. It is surprisingly rare considering its small
size.
.png)
The protruding cells at the edges can perturb some reactions by
inhibiting the birth of a cell in a 3-cell corner. For example, a
clock can be used to suppress the surplus blinker produced by an
F171 conduit, significantly improving the recovery time of the
circuit:
.png)
clock insertion
A uniquely effective method of adding a glider to the
front edge of a salvo, by first constructing a clock, then
converting it to a glider using a one-bit spark. Here it rebuilds
a sabotaged glider in a deep pocket between other gliders:

In 2015 Chris Cain used this reaction to demonstrate conclusively
that any unidirectional glider salvo, no matter how large or
tightly packed, can be constructed by collisions between gliders that
are initially separated by any finite distance. As a corollary,
because all glider syntheses are made up of two to four
unidirectional salvos, any glider-constructible object has a
synthesis that starts with every glider at least N cells away from
every other glider (for any chosen N).
cloverleaf
This name was given by Robert Wainwright to his p2
oscillator washing machine. But Achim Flammenkamp also gave this
name to Achim's p4.
cluster
Any pattern in which each live cell is connected to every
other live cell by a path that does not pass through two consecutive
dead cells. This sense is due to Nick Gotts, but the term has also
been used in other senses, often imprecise.
CNWH
Conweh, creator of the Life universe.
Coe ship
c/2 orthogonally, p16
A puffer engine discovered by Tim
Coe in October 1995.

In December 2015, the Coe ship was discovered in an asymmetric
random soup on Catagolue. This was the first time any non-p4 ship
was discovered in a random asymmetric soup experiment, winning Adam
P. Goucher a 50-euro prize offered by Ivan Fomichev.
Coe's p8
p8
Found by Tim Coe in August 1997.

Collatz 5N+1 simulator
An unknown fate pattern constructed by David
Bell in December 2017 that simulates the Collatz 5N+1 algorithm using
sliding block memory and p1 technology, while always having a
population below 32000.
The algorithm is simple. Starting with a number, if it is even
divide it by 2, otherwise multiply it by 5 and add 1. When this
process is iterated a sequence of numbers is generated. When
starting with the value of 7, it is currently unknown whether or not
the sequence ever forms a cycle.
Because of this the fate of the simulator is also currently
unknown. It may become stable, or become an oscillator with a high
period, or have a bounding box which grows irregularly.
colourised Life
A cellular automaton that is the same as Life
except for the use of a number of different ON states ("colours").
All ON states behave the same for the purpose of applying the Life
rule, but additional rules are used to specify the colour of the
resulting ON cells. Examples are Immigration and QuadLife.
colour of a glider
The colour of a glider is a property of the
glider that remains constant while the glider is moving along a
straight path, but that can be changed when the glider bounces off a
reflector. It is an important consideration when building
something using reflectors.
The colour of a glider can be defined as follows. First choose
some cell to be the origin. This cell is then considered to be
white, and all other cells to be black or white in a checkerboard
pattern. (So the cell with coordinates (m,n) is white if m+n is
even, and black otherwise.) Then the colour of a glider is the
colour of its leading cell when it is in a phase that can be rotated
to look like this:

A reflector that does not change the colour of gliders obviously
cannot be used to move a glider onto a path of different colour than
it started on. But a 90-degree reflector that does change the colour
of gliders is similarly limited, as the colour of the resulting
glider will depend only on the direction of the glider, no matter how
many reflectors are used. For maximum flexibility, therefore, both
types of reflector are required.
Small periodic colour-changing glider reflectors (bouncers) are
known, and also small periodic colour-preserving glider reflectors
(bumpers). Among stable patterns, only a small colour-preserving
reflector (Snark) is known. The smallest known 90-degree
colour-changing reflector is given at the end of the reflector
entry.
component
A partial glider synthesis that can be used in the same
way in multiple glider recipes. A component transforms part of an
object under construction in a well-defined way, without affecting
the rest of the object. For example, this well-known component can
be used to add a hook to any object that includes a protruding
table end, converting it to a long bookend:

"Component" is also used to specify any piece of an object -
spaceship, oscillator, etc. - that can be combined with other
components in specific ways according to a grammar to produce a
variety of objects. The components can either be independent objects
that only occasionally react with each other, or else they can be
fused together to support each other. For example, any
branching spaceship is made up of several components, and there is
a single repeating component in any wicktrailer.
conduit
Any arrangement of still lifes and/or oscillators that
moves an active object to another location, perhaps also transforming
it into a different active object at the same time, but without
leaving any permanent debris (except perhaps gliders, or other
spaceships) and without any of the still lifes or oscillators being
permanently damaged. Probably the most important conduit is the
following remarkable one (Dave Buckingham, July 1996) in which a
B-heptomino is transformed into a Herschel in 59 generations.
Several hundred elementary conduits are now known, with recent
discoveries primarily made via search programs such as CatForce
and Bellman.
confused eaters
p4
Found by Dave Buckingham before 1973.
constellation
A general term for a group of two or more separate
objects, usually small still lifes and low-period oscillators.
Compare pseudo still life.
construction arm
An adjustable mechanism in a universal constructor
that allows new objects to be constructed in any chosen location that
the arm can reach. A construction arm generally consists of a
shoulder containing fixed guns or edge shooters, a movable
construction elbow that slides forward and backward along the
construction lane(s), and in the case of single-arm universal
constructors, a hand target object at the construction site that
can be progressively modified by a slow salvo to produce each
desired object.
construction elbow
One of the components of a construction arm in a
universal constructor. The elbow usually consists of a single
Spartan still life or small constellation. It accepts
elbow operation recipes, in the form of salvos coming from the
construction arm's shoulder.
These recipes may do one of several things: 1) pull the elbow
closer to the shoulder, 2) push the elbow farther from the
shoulder, 3) emit a glider on a particular output lane (while also
optionally pushing or pulling the elbow); 4) create a "hand" target
block or other useful object as a target for output gliders, to one
side of the construction lane; 5) duplicate the elbow, or 6)
destroy the elbow.
Elbows that receive and emit orthogonally-travelling spaceships
instead of gliders are technically possible, but no working examples
are currently known. The discussion below assumes that gliders are
used to communicate between the shoulder, elbow, and hand locations.
If a mechanism can be programmed to generate recipes for at least
the first three options listed above, it is generally capable of
functioning as a universal constructor. The main requirement is
that push and pull elbow operations should be available that are
either minimal (1fd) or the distances should be relatively prime.
Depending on the elbow operation library, there may be only one
type of elbow, or there may be two or more elbow objects, with
recipes that convert between them. The 9hd library had just one
elbow type, a block. The original 10hd library had two elbows,
blocks in mirror-symmetric locations; this was expanded to a larger
list for the 10hd Demonoid. The 0hd Demonoid also has a
multi-elbow recipe library. A slow elbow toolkit may make use of
an even larger number of glider output recipes, because the target
elbow object in that case is not restricted to a single diagonal
line.
If only one colour, parity, or phase of glider can be emitted, then
the mechanism will be limited to producing monochromatic salvos or
monoparity salvos. These are less efficient at most construction
tasks, but are still generally accepted to enable
universal toolkits. See also half-baked knightship.
construction envelope
The region affected by an active reaction, such
as a glider synthesis of an object. The envelope corresponds to
the state-2 blue cells in LifeHistory. See also edgy.
converter
A conduit in which the input object is not of the same
type as the output object. This term tends to be preferred when
either the input object or the output object is a spaceship.
The following diagram shows a p8 pi-heptomino-to-HWSS
converter. This was originally found by Dave Buckingham in a larger
form (using a figure-8 instead of the boat). The improvement
shown here is by Bill Gosper (August 1996). Dieter Leithner has
since found (much larger) oscillators of periods 44, 46 and 60 that
can be used instead of the Kok's galaxy.
.png)
For another periodic converter, see the glider-to-LWSS example in
queen bee shuttle pair. However, many converters are stable.
Examples of elementary conduit converters include BFx59H,
135-degree MWSS-to-G, and 45-degree MWSS-to-G.
The earliest and simplest stable converters known are shown below.
These are an HWSS-to-loaf, MWSS-to-beehive, and LWSS-to-blinker.
These can serve as memory cells, or as the first steps in
constructing objects using salvos.
.png)
copperhead
c/10 orthogonally, p10
The following small c/10
spaceship, discovered by conwaylife.com forum user 'zdr' on 5 March
2016, using a simple depth-first search program. A
glider synthesis was found on the same day.

Later that same month Simon Ekström added a sparky tagalong for
the copperhead to produce the fireship. This allowed for the
construction of c/10 puffers and rakes.
Corder-
Prefix used for things involving switch engines, after
Charles Corderman.
Cordership
Any spaceship based on switch engines. These
necessarily move at a speed of c/12 diagonally with a period of 96 or
a multiple thereof. The first Cordership was constructed by Dean
Hickerson in April 1991, using 13 switch engines. He soon reduced
this to 10, and in August 1993 to 7. In July 1998 he reduced it to
6. In January 2004, Paul Tooke found the 3-engine glide symmetric
Cordership shown below.

At the end of 2017, Aidan F. Pierce discovered a clean
2-engine Cordership. There is also an adjustable-length 4-engine
Cordership found by Michael Simkin, made up of two identical or
mirror-image 2-engine components. The leading pair of switch engines
builds a block trail, which are then deleted by the trailing pair.
Corderships generate sparks which can perturb other objects in
many ways, especially gliders which can reach them from the side or
from behind. Some perturbations reflect gliders back the way they
came, and can be used for constructions such as the caber tosser
and the infinite glider hotel.
cow
c p8 fuse

CP semi-Snark
A period-multiplying colour-preserving signal
conduit found by Tanner Jacobi in October 2017, producing one
output glider for every two input gliders. It is made by replacing
one of the eaters in a Snark with a catalyst found using
Bellman. The catalyst causes the formation of a tub which
requires a second glider to delete. However, this adds 5 ticks to
the repeat time, so that it becomes 48. This is still 3 ticks faster
than the CC semi-Snark.

crane
c/4 diagonally, p4
The following spaceship found by Nicolay
Beluchenko in September 2005, a minor modification of a tubeater
found earlier by Hartmut Holzwart. The wing is of the same form as
in the swan and Canada goose.

cross
p3
Found by Robert Wainwright in October 1989. The members
of this family are all polyominoes.
.png)
In February 1993, Hartmut Holzwart noticed that this is merely the
smallest of an infinite family of p3 oscillators. The next smallest
member is shown below.
.png)
crowd
p3
Found by Dave Buckingham in January 1973.

crystal
A regular growth that is sometimes formed when a stream of
gliders, or other spaceships, is fired into some junk.
The most common example is initiated by the following collision of
a glider with a block. With a glider stream of even period at
least 82, this gives a crystal which forms a pair of beehives for
every 11 gliders which hit it.

cuphook
p3
Found by Rich Schroeppel, October 1970. This is one of
only three essentially different p3 oscillators with only three
cells in the rotor. The others are 1-2-3 and stillater.
.png)
The above is the original form, but it can be made more compact:
.png)
dart
c/3 orthogonally, p3
Found by David Bell, May 1992. A
25-glider recipe for the dart was found in December 2014 by Martin
Grant and Chris Cain, making it the first glider-constructible c/3
spaceship.
de Bruijn graph
As applied to Life, a de Bruijn graph is a graph
showing which pieces can be linked to which other pieces to form a
valid part of a Life pattern of a particular kind.
For example, if we are interested in still lifes, then we could
consider 2×3 rectangular pieces and the de Bruijn graph would show
which pairs of these can be overlapped to form 3×3 squares in which
the centre cell remains unchanged in the next generation.
David Eppstein's search program gfind is based on de Bruijn
graphs.
Deep Cell
A pattern by Jared James Prince, based on David Bell's
unit Life cell, in which each unit cell simulates two Life cells,
in such a way that a Life universe filled with Deep Cells simulates
two independent Life universes running in parallel.
In fact, a Life universe filled with Deep Cells can simulate
infinitely many Life universes, as follows. Let P1, P2, P3, ...
be a sequence of Life patterns. Set the Deep Cells to run a
simulation of P1 in parallel with a simulation of a universe filled
with Deep Cells, with these simulated Deep Cells running a simulation
of P2 in parallel with another simulation of a universe filled with
Deep Cells, with these doubly simulated Deep Cells simulating P3 in
parallel with yet another universe of Deep Cells, and so on.
Deep Cell is available from http://psychoticdeath.com/life.htm.
Demonoid
The first self-constructing diagonal spaceship. A 0hd
Demonoid was completed by Chris Cain in December 2015, shortly after
a much larger 10hd version was constructed the previous month in
collaboration with Dave Greene. The 0hd spaceship fits in a bounding
box about 55,000 cells square, and displaces itself by 65 cells
diagonally every 438,852 generations.
The first 0hd Demonoid was fired by a gun. No spaceship gun
pattern had previously been completed before the first appearance of
the actual spaceship.
In June 2017 Dave Greene completed a much simpler single-channel
Demonoid using a temporary lossless elbow, which displaces itself
79 cells diagonally every 1,183,842 ticks. This was an improvement
in terms of design complexity, but not in terms of speed, population,
or bounding box. However, all of these could be further optimized.
A smaller Hashlife-friendly single-channel Demonoid design was
completed in 2018.
demultiplexer
A simple Herschel circuit consisting of three
eater1s, found by Brice Due in August 2006. An input Herschel
places a boat in a location accessible to an input glider. If the
boat is present, a one-time turner reaction occurs and the glider
is turned 90 degrees onto a new lane.

If the Herschel and boat are removed from the above pattern, the
glider passes cleanly through the circuit. It can be used as the "0"
output of a one-bit memory cell, where the 90-degree output would
be the "1" output. This was the method used to store presence or
absence of neighbor metacells in the p1 megacell.
density
The density of a pattern is the limit of the proportion of
live cells in a (2n+1)×(2n+1) square centred on a particular cell as
n tends to infinity, when this limit exists. (Note that it does not
make any difference what cell is chosen as the centre cell. Also
note that if the pattern is finite then the density is zero.) There
are other definitions of density, but this one will do here.
In 1994 Noam Elkies proved that the maximum density of a stable
pattern is 1/2, which had been the conjectured value. See the paper
listed in the bibliography. Marcus Moore provided a simpler proof in
1995, and in fact proves that a still life with an m × n
bounding box has at most (mn+m+n)/2 cells.
But what is the maximum average density of an oscillating pattern?
The answer is conjectured to be 1/2 again, but this remains unproved.
The best upper bound so far obtained is 8/13 (Hartmut Holzwart,
September 1992).
The maximum possible density for a phase of an oscillating
pattern is also unknown. An example with a density of 3/4 is known
(see agar), but densities arbitrarily close to 1 may perhaps be
possible.
dependent conduit
A Herschel conduit in which the input Herschel
interacts with catalysts in the first few ticks. The standard
interaction actually starts at T=-3, before the Herschel is
completely formed. Compare independent conduit. The Herschel is
prevented from emitting its first natural glider. This is useful
in cases where the previous conduit cannot survive a first natural
glider emitted from its output Herschel.
This term is somewhat confusing, since it is actually the previous
conduit that depends on the dependent conduit to suppress the
problematic glider. Dependent conduits such as the F166 and
Lx200 do not actually depend on anything. They can be freely
connected to any other conduits that fit, as long as the output
Herschel evolves from its standard great-grandparent. As of this
writing, the Fx158 is the only known case where a conduit's output
Herschel has an alternate great-grandparent, which is incompatible
with dependent conduits' initial transparent block.
destructive read
The most common type of test reaction in
memory cell circuitry. Information is stored in a memory cell by
placing objects in known positions, or by changing the state of a
stable or periodic toggle circuit. A destructive-read test
consists of sending one or more signals to the memory cell. A
distinct output signal is produced for each possible state of the
memory cell, which is reset to a known "zero" or "rest" state. See
for example boat-bit, keeper, and demultiplexer.
To permanently store information in a destructive-read memory cell,
the output signal(s) must be used, in part, to send appropriate
signals back to the memory cell to restore its state to its previous
value. With output looped back to input, this larger composite
circuit then effectively becomes a non-destructive read memory
cell.
destructor arm
A dedicated construction arm in the Gemini
spaceship, used only for removing previously active circuitry once
it is no longer needed. More generally, any circuitry in a
self-constructing pattern dedicated exclusively to cleanup.
diamond ring
p3
Found by Dave Buckingham in 1972.

diehard
Any pattern that vanishes, but only after a long time. The
following example vanishes in 130 generations, which is probably the
limit for patterns of 7 or fewer cells. Note that there is no limit
for higher numbers of cells. E.g., for 8 cells we could have a
glider heading towards an arbitrarily distant blinker.

dinner table
p12
Found by Robert Wainwright in 1972.

dirty
Opposite of clean. A reaction which produces a large amount
of complicated junk which is difficult to control or use is said to
be dirty. Many basic puffer engines are dirty and need to be
tamed by accompanying spaceships in order to produce clean
output. Similarly, a dirty conduit is one that does not recover
perfectly after the passage of a signal; one or more extra ash
objects are left behind (or more rarely a catalyst is damaged) and
additional signals must be used to clean up the circuit before it can
be re-used.
diuresis
p90
Found by David Eppstein in October 1998. His original
stabilization used pentadecathlons. The stabilization with
complicated still lifes shown here (in two slightly different
forms) was found by Dean Hickerson the following day. The name is
due to Bill Gosper (see kidney).

dormant
An object that is either stable or oscillates without
producing any output, until it is triggered by an appropriate
signal, which then produces some desired action. For example,
freeze-dried objects are dormant until the arrival of a particular
glider.
do-see-do
The following reaction, found by David Bell in 1996, in
which two gliders appear to circle around each other as they are
reflected 90 degrees by a twin bees shuttle. Four copies of the
reaction can be used to create a p92 glider loop which repeats the
do-see-do reaction forever.

double-barrelled
Of a gun, emitting two streams of spaceships (or
rakes) every period. For examples, see B-52 bomber,
Simkin glider gun, and p246 gun. In most cases, the two streams
are alternately emitted 1/2 period apart. It is also possible for
the two streams to be emitted simultaneously, as in this
double-barrelled glider gun by Bill Gosper:

double block reaction
A certain reaction that can be used to
stabilize the twin bees shuttle (qv). This was discovered by David
Bell in October 1996.
The same reaction sometimes works in other situations, as shown in
the following diagram where a pair of blocks eats an R-pentomino
and a LWSS. (The LWSS version was known at least as early 1994,
when Paul Callahan saw it form spontaneously as a result of firing an
LWSS stream at some random junk.)
double ewe
p3
Found by Robert Wainwright before September 1971.

dove
The following induction coil, found in 2015 to be a possible
active reaction for the input or output of a converter.

dragon
c/6 orthogonally, p6
This spaceship, discovered by Paul
Tooke in April 2000, was the first known c/6 spaceship. With 102
cells, it was the smallest known orthogonal c/6 spaceship until
Hartmut Holzwart discovered 56P6H1V0 in April 2009.

drain trap
= paperclip. This term is no longer in use.
drifter
A perturbation moving within a stable pattern. Dean
Hickerson has written a search program to search for drifters, with
the hope of finding one which could be moved around a track. Because
drifters can be very small, they could be packed more tightly than
Herschels, and so allow the creation of oscillators of periods
not yet attained, and possibly prove that Life is omniperiodic.
Hickerson has found a number of components towards this end, but it
has proved difficult to change the direction of movement of a
drifter, and so far no complete track has been found. However,
Hickerson has had success using the same program to find eaters
with novel properties, such as sparking eaters and the ones shown
in diuresis.
duoplet
A diagonal two-bit spark produced by many oscillators and
eater reactions. Among other uses, it can reflect gliders 90
degrees. The following pattern shows an eater5 eating gliders and
producing duoplets which are then used to reflect a separate glider
stream. If only one glider is present, the eater5 successfully
absorbs it, so this mechanism may be considered to be a simple AND
gate.

dying spark
See spark. A spark by definition dies out completely
after some number of ticks.
early universe
Conway's somewhat confusing term for sparse Life.
eater
Any still life that has the ability to interact with certain
patterns without suffering any permanent damage. (If it doesn't
suffer even temporary damage then it may be referred to as a rock.)
The eater1 is a very common eater, and the term "eater" is often
used specifically for this object. Other eaters include eater2,
eater3, eater4, and eater5, and many hundreds of others are
known. Below is a complex eater found by Dean Hickerson in 1998
using his dr search program. It takes 25 ticks to recover
after feasting on a glider:

Some common still lifes can act as eaters in some situations,
such as the block, ship, and tub. In fact the block was the
first known eater, being found capable of eating beehives from a
queen bee.
eater1
p1
Usually simply called an eater, and also called a
fishhook.
.png)
This eater can be constructed using a simple two-glider collision,
as shown in stamp collection. It is often modified in various
ways, or welded to other objects, to allow tighter packing of
circuits or to allow a signal stream to pass close by. See
clearance for an eater1 variant that is 1hd shorter to the
southeast than the standard fishhook form. An eater1 can also be
used as a 90-degree one-time turner.
Its ability to eat various objects was discovered by Bill Gosper in
1971. The fishhook eater can consume a glider, a LWSS, and a
MWSS as shown below. It is not able to consume an HWSS, however.
See honey bit or killer toads for that.
.png)
eater2
p1
This eater was found by Dave Buckingham in the 1970s.
Mostly it works like the ordinary eater1 but with two slight
differences that make it useful despite its size: it takes longer to
recover from each bite, and it can eat objects appearing at two
different positions.
.png)
The first property means that, among other things, it can eat a
glider in a position that would destroy an eater1. This novel
glider-eating action is occasionally of use in itself, and combined
with the symmetry means that an eater2 can eat gliders travelling
along four adjacent glider lanes, as shown below.
The following eater2 variant (Stephen Silver, May 1998) can be
useful for obtaining smaller bounding boxes. A more compact
variant with the same purpose can be seen under gliderless.
.png)
eater3
p1
This large symmetric eater, found by Dave Buckingham,
has a very different eating action from the eater1 and eater2.
The loaf can take bites out things, being flipped over in the
process. The rest of the object merely flips it back again.

eater4
p1
Another eater by Dave Buckingham, which he found in
1971, but did not recognize as an eater until 1975 or 1976. It can't
eat gliders, but it can be used for various other purposes. The
four NE-most centre cells regrow in a few generations after being
destroyed by taking a bite out of something, such as suppressing half
of a developing traffic light as it does in the
p29 pentadecathlon hassler.

eater5
p1
A compound eater that can eat gliders coming from two
different directions. Also called the tub-with-tail eater (TWIT), it
is often placed along the edges of glider lanes to suppress
unwanted gliders in conduits. Below is the standard form, a compact
form with a long hook, and an often-useful conjoined form found
with Bellman. The sidesnagger is a Spartan constellation that
has a similar glider-absorbing function, using a loaf. See also
7x9 eater.

With gliders from either direction, the eater5's eating reaction
creates a spark that can be used to reflect other gliders. See the
example pattern in duoplet, or advance any of the topmost three
gliders in the above pattern by two ticks.
eater/block frob
p4
Found by Dave Buckingham in 1976 or earlier.

eater plug
p2
Found by Robert Wainwright, February 1973.

ecologist
c/2 orthogonally, p20
This consists of the classic
puffer train with a LWSS added to suppress the debris. See also
space rake.

edge-repair spaceship
A spaceship which has an edge that possesses
no spark and yet is able to perturb things because of its ability
to repair certain types of damage to itself. The most useful
examples are the following two small p3 c/3 spaceships:
.png)
These were found by David Bell in 1992, but the usefulness of the
edge-repair property wasn't recognised until July 1997. The
following diagram (showing an edge-repair spaceship deleting a
Herschel) demonstrates the self-repairing action.
.png)
In October 2000, David Bell found that a T-tetromino component of a
c/4 spaceship can also be self-repairing. Stephen Silver noticed
that it could be used to delete beehives and, in November 2000, found
the smallest known c/4 spaceship with this edge-repair component - in
fact, two copies of the component:
.png)
edge shooter
A gun or signal circuit that fires its gliders (or
whatever) right at the edge of the pattern, so that it can be used to
fire them closely parallel to others. This is useful for
constructing complex guns. Compare glider pusher, which can in
fact be used for making edge shooters.
The following diagram shows a p46 edge shooter found by Paul
Callahan in June 1994.

Stable edge shooters became possible with the development of
Herschel circuitry. For example, NW31, BNE14T30, RNE-19T84,
and the high-clearance Fx119 inserter are often used in
shotguns for complex salvos. Composite edge-shooter circuits with
arbitrarily high clearance can be constructed.
edge spark
A spark at the side of a spaceship that can be used to
perturb things as the spaceship passes by.
edgy
In slow salvo terminology, an edgy glider construction recipe
is one that places its final product at or very near the edge of its
construction envelope. Similarly, an edgy factory will place its
output object in an accessible location near the edge of its
reaction envelope.
egg
= non-spark. This term is no longer in use.
E-heptomino
Name given by Conway to the following heptomino.

elbow ladder
Scot Ellison's name for the type of pattern he created
in which one or more gliders shuttle back and forth (using the
kickback reaction) deleting the output gliders from a pair of
slide guns.
electric fence
p5
A stabilization of ants. Dean Hickerson,
February 1993.
elementary
Not reducible to a combination of smaller parts.
Elementary spaceships in particular are usually those found by
search programs, and they can't be subdivided into smaller
spaceships, tagalongs, and supporting reactions, as contrasted with
engineered macro-spaceships.
elementary conduit
A conduit with no recognizable active signal
stage besides its input and output. An early example still very
commonly used is Buckingham's BFx59H, which transforms a
B-heptomino into an inverted Herschel in 59 ticks. The BFx59H
elementary conduit is a component in many of the original universal
toolkit of Herschel conduits. An extension of the same naming
convention is used for elementary conduits, with the first and last
letters of the name specifying the input and output signal objects.
As with Herschels, an arbitrary orientation and center point is
chosen for each object. "Fx" means the signal moves forward and
produces a mirror-image output. See Herschel conduit for further
details.
Theoretically an elementary conduit may become a composite conduit,
if another conduit can be found that shares the beginning or end of
the conduit in question. In practice this happens only rarely,
because many of the most likely branch points have already been
identified: glider (G), LWSS (L) or MWSS (M), Herschel (H),
B-heptomino (B), R-pentomino (R), pi-heptomino (P),
queen bee shuttle (Q), century or bookend (C), dove (D), and
wing (W). A Herschel descendant might qualify, due to the
elementary conduit that can be seen in the p184 gun. However,
there are very few simple conduits that produce Herschel descendants
without Herschels, so in practice this is not a useful branch point.
elevener
p1

Elkies' p5
p5
Found by Noam Elkies in 1997.

emu
Dave Buckingham's term for a Herschel loop that does not emit
gliders (and so is "flightless"). All known Herschel loops of
periods 52, 57, 58, 59 and 61 are emus. See also Quetzal.
emulator
Any one of three p4 oscillators that produce sparks
similar to those produced by LWSS, MWSS and HWSS. See
LW emulator, MW emulator and HW emulator. Larger emulators are
also possible, but they require stabilizing objects to suppress their
non-sparks and so are of little use. The emulators were discovered
by Robert Wainwright in June 1980.
engineless
A rake or puffer which does not contain a specific
engine for its operation. Instead it depends on perturbations of
gliders or other objects by passing spaceships. The period of such
objects is often adjustable, and in some cases the speed as well. An
early example was the creation of c/5 rakes in September 1997, using
gliders circulating among a convoy of c/5 spaceships. More recently,
the passing spaceships themselves are also constructed, as in the
Caterloopillar.
en retard
p3
Found by Dave Buckingham, August 1972.

Enterprise
c/4 diagonally, p4
Found by Dean Hickerson, March 1993.

Eureka
p30
A pre-pulsar shuttle found by Dave Buckingham in
August 1980. A variant is obtained by shifting the top half two
spaces to either side.
evolution
The process or result of running one or more generations of
an object. For example, a row of 10 cells evolves into a
pentadecathlon.
evolutionary factor
For an unstable pattern, the time to
stabilization divided by the initial population. For example, the
R-pentomino has an evolutionary factor of 220.6, while bunnies
has an evolutionary factor of 1925.777... The term is no longer in
use.
exhaust
The debris or smoke left behind by a puffer, especially
if the debris is dirty and takes many generations to settle. The
term is not usually used for the objects created by clean puffers.
exponential filter
A toolkit developed by Gabriel Nivasch in 2006,
enabling the construction of patterns with asymptotic population
growth matching O((log log ... log(t))) for any number of nested log
operations. See also quadratic filter, recursive filter.
extremely impressive
p6
Found by Dave Buckingham, August 1976.

F171
An elementary conduit, the seventeenth Herschel conduit,
discovered by Brice Due in August 2006 in a search using only
eaters as catalysts. This was the first new Herschel conduit
discovery since 1998. After 171 ticks, it produces a Herschel at
(29, -17) relative to the input. A ghost Herschel in the pattern
below marks the output location:

The conduit's recovery time is 227 ticks, slower than many of the
original sixteen conduits because of the delayed destruction of a
temporary blinker, though the circuit itself is clearly Spartan.
The recovery time can be improved to 120 ticks by adding sparkers
of various periods to suppress the blinker. See clock for a
period-2 example.
The central eater in the group of three to the northwest can be
removed to release an additional glider output signal on a
transparent lane.
factory
Another word for gun, but not used in the case of glider
guns. The term is also used for a pattern that repeatedly
manufactures objects other than spaceships or rakes. In this
case the new objects do not move out of the way, and therefore must
be used up in some way before the next one is made. The following
shows an example of a p144 gun which consists of a p144 block factory
whose output is converted into gliders by a p72 oscillator.

This gun is David Bell's improvement of the one Bill Gosper found in
July 1994. The p72 oscillator is by Robert Wainwright in 1990, and
the block factory is Achim's p144 minus one of its stabilizing
blocks. For a block factory using stable components and triggered by
an input Herschel, see also keeper.
fanout
A mechanism that emits two or more objects of some type for
each one that it receives. Typically the objects are gliders or
Herschels; glider duplicators are a special case.
Fast Forward Force Field
The following reaction found by Dieter
Leithner in May 1994. In the absence of the incoming LWSS the
gliders would simply annihilate one another, but as shown they allow
the LWSS to advance 11 spaces in the course of the next 6
generations.

The illusion of super-light-speed travel is caused by an LWSS that
is always created, but is then destroyed in some cases, by a signal
catching up to it from behind that necessarily never travels faster
than the speed of light. It is not possible to make any use of the
apparent super-light-speed signal. The front end of an output LWSS
can't be distinguished from the alternative dying spark output
until several more ticks have passed. Not surprisingly, this extra
time is enough to drop the average speed of information transmission
safely below c.
Leithner named the Fast Forward Force Field in honour of his
favourite science fiction writer, the physicist Robert L. Forward.
See also star gate and speed booster.
fate
The result of evolving a pattern until its final behaviour is
known. This answers such questions such as whether or not the
pattern remains finite, what its growth rate is, what period the
final state may settle into, and what its final census is. All
small Life objects seem to eventually settle down into a mix of
oscillators, simple spaceships, and occasionally small puffers. See
methuselah, soup, ash.
Most sufficiently large random patterns are expected to grow
forever due to the production of switch engines at their boundary.
Engineered Life objects - and therefore also sufficiently large and
unlikely random patterns - can have more interesting behaviour, such
as breeders, sawtooths, and prime calculators. Some objects have
even been constructed or designed having an unknown fate.
featherweight spaceship
= glider
fencepost
Any pattern that stabilizes one end of a wick.
Fermat prime calculator
A pattern constructed by Jason Summers in
January 2000 that exhibits infinite growth if and only if there are
no Fermat primes greater than 65537. The question of whether or not
it really does exhibit infinite growth is therefore equivalent to a
well-known and long-standing unsolved mathematical problem. It will,
however, still be growing at generation 102585827975. The pattern is
based on Dean Hickerson's primer and caber tosser patterns and a
p8 beehive puffer by Hartmut Holzwart.
F-heptomino
Name given by Conway to the following heptomino.

filter
Any oscillator used to delete some but not all of the
spaceships in a stream. An example is the blocker, which can be
positioned so as to delete every other glider in a stream of period
8n+4, and can also do the same for LWSS streams. Other examples
are the MW emulator and T-nosed p4 (either of which can be used
to delete every other LWSS in a stream of period 4n+2), the
fountain (which does the same for MWSS streams) and a number of
others, such as the p6 pipsquirter, the pentadecathlon and the
p72 oscillator shown under factory. Another example, a p4
oscillator deleting every other HWSS in a stream of period 4n+2, is
shown below. (The p4 oscillator here was found, with a slightly
larger stator, by Dean Hickerson in November 1994.)

filter stream
A stream of spaceships in which there are periodic
gaps in the stream. This can thin out another crossing stream by
deleting the spaceships in the second stream except where the gaps
occur. The filter stream is not affected by the deletions so that
the same stream can thin out multiple other streams. The
Caterpillar uses filter streams of MWSSs in which there is a gap
every 6 spaceships. Here is part of a filter stream that thins a
glider stream by 2/3:

finger
A protruding cell in an oscillator or dying spark, with
the ability to modify a nearby active reaction. Like a thumb, a
finger cell appears at the edge of a reaction envelope and is the
only live cell in its row or column. The finger spark remains alive
for two ticks before dying, whereas a thumb cell dies after one tick.
Because the key cell is kept alive for an extra tick, an alternate
technical term is "held (orthogonal) bit spark". A "held diagonal
bit spark" is not possible in B3/S23 for obvious reasons.
fire
An encoded signal used in combination with push and pull
elbow operations in a simple construction arm. When a FIRE
signal is sent, the construction-arm elbow produces an output glider,
usually at 90 degrees from the construction arm. This terminology is
generally used when there is only a single recipe for such a glider
output, or only one recipe for each glider colour (e.g., FIRE WHITE,
FIRE BLACK).
fireship
c/10 orthogonally, p10
A variant of the copperhead with
a trailing component that emits several large sparks, discovered by
Simon Ekström on 20 March 2016. The interaction between the
copperhead and the additional component is minimal enough that the
extension technically fits the definition of a tagalong. However,
the extension slightly modifies two of the phases of the spaceship,
starting two ticks after the phase shown below, so it's also valid to
classify the fireship as a distinct spaceship.

fire-spitting
p3
Found by Nicolay Beluchenko, September 2003.

fish
A generic term for LWSS, MWSS and HWSS, or, more
generally, for any spaceship. In recent years *WSS is much more
commonly used to refer to the small orthogonal c/2 spaceships.
fleet
p1
A common formation of two ship-ties.

flip-flop
Any p2 oscillator. However, the term is also used in two
more specific (and non-equivalent) senses: (a) any p2 oscillator
whose two phases are mirror images of one another, and (b) any p2
oscillator in which all rotor cells die from underpopulation. In
the latter sense it contrasts with on-off. The term has also been
used even more specifically for the 12-cell flip-flop shown under
phoenix.
flip-flops
Another name for the flip-flop shown under phoenix.
flotilla
A spaceship composed of a number of smaller interacting
spaceships. Often one or more of these is not a true spaceship and
could not survive without the support of the others. The following
example shows an OWSS escorted by two HWSS.

fly
A certain c/3 tagalong found by David Bell, April 1992. Shown
here attached to the back of a small spaceship (also by Bell).

fly-by deletion
A reaction performed by a passing convoy of
spaceships which deletes a common stationary object without harming
the convoy. Fly-by deletion is often used in the construction of
puffers and spaceships to clean up unwanted debris.
For c/2 convoys this is not usually difficult since the LWSS,
MWSS, and HWSS spaceships have such useful sparks. However,
some objects are more difficult to delete. For example, deleting a
tub appears to require an unusual p4 spaceship.
The deletion of a pond appears to require a convoy which is 89
cells in width containing a very unusual p4 spaceship which has 273
cells. There are small objects which have no known fly-by deletion
reactions. However, as in the case of reanimation, hitting them
with the output of rakes is an effective brute force method.
fore and back
p2
Compare snake pit. Found by Achim Flammenkamp,
July 1994.

forward glider
A glider which moves at least partly in the same
direction as the puffer(s) or spaceship(s) under consideration.
fountain
p4
Found by Dean Hickerson in November 1994, and named by
Bill Gosper. See also filter and superfountain.

fourteener
p1

fox
p2
This is the smallest asymmetric p2 oscillator. Found by
Dave Buckingham, July 1977.

freeze-dried
A term used for a glider constructible seed that can
activated in some way to produce a complex object. For example, a
"freeze-dried salvo" is a constellation of constructible objects
which, when triggered by a single glider, produces a unidirectional
glider salvo, and nothing else. Freeze-dried salvos can be useful
in slow salvo constructions, especially when an active circuit has
to destroy or reconstruct itself in a limited amount of time.
Gradual modification by a construction arm may be too slow, or the
circuit doing the construction may itself be the object that must be
modified.
The concept may be applied to other types of objects. For example,
one possible way to build a gun for a waterbear would be to program
a construction arm to build a freeze-dried waterbear seed, and then
trigger it when the construction is complete.
French kiss
p3
Found by Robert Wainwright, July 1971.

For many years this was one of the best-known small oscillators with
no known glider synthesis. In October 2013 Martin Grant completed
a 23-glider construction.
frog II
p3
Found by Dave Buckingham, October 1972.

frothing puffer
or a frothing spaceship
is a
puffer (or spaceship) whose back end appears to be unstable and
breaking apart, but which nonetheless survives. The exhaust
festers and clings to the back of the puffer/spaceship before
breaking off. The first known frothing puffers were c/2, and most
were found by slightly modifying the back ends of p2 spaceships. A
number of these have periods which are not a multiple of 4 (as with
some line puffers). Paul Tooke has also found c/3 frothing
puffers.
The following p78 c/2 frothing puffer was found by Paul Tooke in
April 2001.

full diagonal
Diagonal distance measurement, abbreviated "fd", often
appropriate when a construction arm elbow or similar
diagonally-adjustable mechanism is present.
fumarole
p5
Found by Dean Hickerson in September 1989. In terms of
its 7×8 bounding box this is the smallest p5 oscillator.

fuse
A wick burning at one end. For examples, see baker,
beacon maker, blinker ship, boat maker, cow, harvester,
lightspeed wire, pi ship, reverse fuse, superstring and
washerwoman. Useful fuses are usually clean, but see also
reburnable fuse.
A fuse can burn arbitrarily slowly, as demonstrated by the
example Blockic fuse below. A signal, alternating between
glider and MWSS form, travels up and down between two rows of
blocks in a series of one-time turner reactions. The spacing
shown here causes the fuse to burn 24 cells to the right every 240
generations, for a speed of c/10. Moving the bottom half further
from the top half by any even number of cells will slow down the
burning even further.
Fx119
An elementary conduit, one of the original sixteen
Herschel conduits, discovered by Dave Buckingham in September 1996.
After 119 ticks, it produces an inverted Herschel at (20, 14)
relative to the input. Its recovery time is 231 ticks; this can be
reduced somewhat by suppressing the output Herschel's glider, or by
adding extra catalysts to make the reaction settle more quickly. A
ghost Herschel in the pattern below marks the output location:

Fx119 inserter
A Herschel-to-glider converter and edge shooter
based on an Fx119 Herschel conduit:

This edge shooter has an unusually high 27hd clearance, one of
the highest known for a single small component. The only known
higher-clearance edge shooters are injectors making use of multiple
interacting spaceships. This makes the Fx119 inserter ideal for the
construction of wide convoys whose total width can fit within its
clearance distance.
The component creates a large cloud of smoke behind its emitted
glider which lasts for over 90 generations. In spite of this, many
tightly packed convoys can be made by injecting later gliders behind
others in the convoy, helped along by the insertion reaction which is
able to catch up to the existing gliders. The Fx119 inserter can
place a glider on the same lane as a passing glider and as close as
15 ticks behind, which is only one step away from the minimum
possible following distance.
Fx176
A composite conduit, one of the original sixteen
Herschel conduits, discovered by Paul Callahan in October 1997. It
is made up of three elementary conduits, HF95P + PF35W + WFx46H.
After 176 ticks, it produces an inverted Herschel at (45, 0)
relative to the input. The recovery time of the standard form
shown here is 92 ticks, but see the PF35W entry for a variant
discovered in November 2017 that lowers the repeat time to 73 ticks.
A ghost Herschel in the pattern below marks the output location.

Fx77
An elementary conduit, one of the original sixteen
Herschel conduits, discovered by Dave Buckingham in August 1996.
After 77 ticks, it produces an inverted Herschel at (25, -8)
relative to the input. Its recovery time is 61 ticks; this can be
reduced slightly by suppressing the output Herschel's glider, as in
the L112 case. A pipsquirter can replace the blinker-suppressing
eater to produce an extra glider output. It is one of the simplest
known Spartan conduits, and one of the few elementary conduits in
the original set of sixteen.
In January 2016, Tanner Jacobi discovered a Spartan method of
extracting an extra glider output (top variant below). A
ghost Herschel marks the output location for each variant.

Gabriel's p138
p138
The following oscillator found by Gabriel
Nivasch in October 2002.

Garden of Eden
A configuration of ON and OFF cells that can only
occur in generation 0. (This term was first used in connection with
cellular automata by John W. Tukey, many years before Life.) It was
known from the start that there are Gardens of Eden in Life, because
of a theorem by Edward Moore that guarantees their existence in a
wide class of cellular automata. Explicit examples have since been
constructed, the first by Roger Banks, et al. at MIT in 1971. This
example was 9 × 33. In 1974 J. Hardouin-Duparc et al. at the
University of Bordeaux 1 produced a 6 × 122 example. The following
shows a 12 × 12 example found by Nicolay Beluchenko in February 2006,
based on a 13 × 12 one found by Achim Flammenkamp in June 2004.
.png)
Below is a 10×10 Garden of Eden found by Marijn Heule, Christiaan
Hartman, Kees Kwekkeboom, and Alain Noels in 2013 using SAT-solver
techniques. An exhaustive search of 90-degree rotationally symmetric
10×10 patterns was possible because the symmetry reduces the number
of unknown cells by a factor of four.
.png)
Steven Eker has since found several asymmetrical Gardens of Eden
that are slightly smaller than this in terms of bounding box area.
Patterns have also been found that have only Garden of Eden
parents. For related results see grandparent.
Gemini
(5120,1024)c/33699586 obliquely, p33699586
The first
self-constructing spaceship, and also the first oblique
spaceship. It was made public by Andrew Wade on 18 May 2010. It was
the thirteenth explicitly constructed spaceship velocity in Life, and
made possible an infinite family of related velocities. The Gemini
spaceship derives its name from the Latin "gemini", meaning twins,
describing its two identical halves, each of which contains three
Chapman-Greene construction arms. A tape of gliders continually
relays between the two halves, instructing each to delete its parent
and construct a daughter configuration.
Geminoid
A type of self-constructing circuitry that borrows key ideas
from Andrew Wade's Gemini spaceship, but with several
simplifications. The main feature common to the Gemini spaceship is
the construction recipe encoding method. Information is stored
directly, and much more efficiently, in the timings of moving
gliders, rather than in a static tape with 1s and 0s encoded by the
presence of small stationary objects.
Unlike the original Gemini, Geminoids have ambidextrous
construction arms, initially using glider pairs on two lanes
separated by 9hd, 10hd, or 0hd. The design was the basis for the
linear propagator and the Demonoids. A more recent development
is a Geminoid toolkit using a single-channel construction arm,
which allows for the possibility of multiple elbows with no loss of
efficiency, or the construction of temporary lossless elbows.
Compare slow elbow.
Other new developments that could be considered part of the
extended "Geminoid" toolkit include freeze-dried construction
salvos and seeds, used when objects must be built within a short time
window, and self-destruct circuits, which are used as an alternative
to a destructor arm to clean up temporary objects in a similarly
short window.
generation
The fundamental unit of time. The starting pattern is
generation 0.
germ
p3
Found by Dave Buckingham, September 1972.

ghost Herschel
A dying spark made by removing one cell from the
Herschel heptomino. This particular spark has the advantage that,
when placed in a conduit to mark the location of an input or output
Herschel, it disappears cleanly without damaging adjacent catalysts,
even in dependent conduits with a block only two cells away.

GIG
A glider injection gate. This is a device for injecting a
glider into a glider stream. The injected glider is synthesized
from one or more incoming spaceships assisted by the presence of
the GIG. (This contrasts with some other glider injection reactions
which do not require a GIG, as in inject.) Gliders already in the
glider stream pass through the GIG without interfering with it. A
GIG usually consists of a small number of oscillators.
For example, in July 1996 Dieter Leithner found the following
reaction which allows the construction of a pseudo-period 14 glider
stream. It uses two LWSS streams, a pentadecathlon and a
volcano.

Glider injection gates are useful for building glider guns with
pseudo-periods that are of the form nd, where n is a positive
integer, and d is a proper divisor of some convenient base gun period
(such as 30 or 46), with d > 13.
glider
c/4 diagonally, p4
The smallest, most common and first
discovered spaceship. This was found by Richard Guy in 1970 while
Conway's group was attempting to track the evolution of the
R-pentomino. The name is due in part to the fact that it is
glide symmetric. (It is often stated that Conway discovered the
glider, but he himself has said it was Guy. See also the cryptic
reference ("some guy") in Winning Ways.)

The term "glider" is also occasionally (mis)used to mean "spaceship".
glider-block cycle
An infinite oscillator based on the following
reaction (a variant of the rephaser). The oscillator consists of
copies of this reaction displaced 2n spaces from one another (for
some n>6) with blocks added between the copies in order to cause the
reaction to occur again halfway through the period. The period of
the resulting infinite oscillator is 8n-20. (Alternatively, in a
cylindrical universe of width 2n the oscillator just consists of two
gliders and two blocks.)

glider duplicator
Any reaction in which one input glider is
converted into two output gliders. This can be done by oscillators
or spaceships, or by Herschel conduits or other signal
circuitry such as the stable example shown under splitter. The
most useful glider duplicators are those with low periods.
The following period 30 glider duplicator demonstrates a simple
mechanism found by Dieter Leithner. The input glider stream comes in
from the upper left, and the output glider streams leave at the upper
and lower right. One of the output glider streams is inverted, so an
inverting reflector is required to complete the duplicator. To
produce non-parallel output, an inline inverter could be
substituted for the northmost p30 glider gun.

Spaceship convoys that can duplicate gliders are very useful
since they (along with glider turners) provide a means to clean up
many dirty puffers by duplicating and turning output gliders so as to
impact into the exhaust to clean it up.
Glider duplicators and turners are known for backward gliders using
p2 c/2 spaceships, and for forward gliders using p3 c/3 spaceships.
These are the most general duplicators for these speeds.
glider gun
A gun that fires gliders. For examples, see
Gosper glider gun, Simkin glider gun, new gun, p45 gun.
True-period glider guns are known for some low periods, and for all
periods over 53 using Herschel conduit technology. See true
for a list of known true-period guns. The lowest true-period gun
possible is the p14 gun since that is the lowest possible period
for any glider stream, but no example has yet been found.
Pseudo-period glider guns are known for every period above 13.
These are made by using multiple true-period guns of some multiple of
the period, and glider injection methods to fill in the gaps.
glider injection gate
= GIG
gliderless
A gun is said to be gliderless if it does not use
gliders. The purist definition would insist that a glider does not
appear anywhere, even incidentally. For a long time the only known
way to construct LWSS, MWSS and HWSS guns involved gliders, and
it was not until April 1996 that Dieter Leithner constructed the
first gliderless gun (a p46 LWSS gun).
In October 2017 Matthias Merzenich used two copies of
Tanner's p46 to create a p46 MWSS gun. This is the smallest known
gliderless gun, and also the smallest known MWSS gun.

glider pusher
An arrangement of a queen bee shuttle and a
pentadecathlon that can push the path of a passing glider out by
one half-diagonal space. This was found by Dieter Leithner in
December 1993 and is shown below. It is useful for constructing
complex guns where it may be necessary to produce a number of
gliders travelling on close parallel paths. See also edge shooter.

gliders by the dozen
stabilizes at time 184
In early references
this is usually shown in a larger form whose generation 1 is
generation 8 of the form shown here.

glider stopper
A Spartan logic circuit discovered by Paul Callahan
in 1996. It allows a glider signal to pass through the circuit,
leaving behind a beehive that can cleanly absorb a single glider from
a perpendicular glider stream. Two optional glider outputs are
also shown. The circuit can't be re-used until the beehive "bit" is
cleared by the passage of at least one perpendicular input. A
similar mechanism discovered more recently is shown in the
beehive stopper entry.

glider synthesis
Construction of an object by means of glider
collisions. It is generally assumed that the gliders should be
arranged so that they could come from infinity. That is, gliders
should not have had to pass through one another to achieve the
initial arrangement.
Glider syntheses for all still lifes and known oscillators with
at most 14 cells were found by Dave Buckingham. As of June 2018,
this limit has been increased to 18 cells.
Perhaps the most interesting glider syntheses are those of
spaceships, because these can be used to create corresponding
guns and rakes. Many of the c/2 spaceships that are based on
standard spaceships have been synthesized, mostly by Mark Niemiec.
In June 1998 Stephen Silver found syntheses for some of the
Corderships (although it was not until July 1999 that Jason Summers
used this to build a Cordership gun). In May 2000, Noam Elkies
suggested that a 2c/5 spaceship found by Tim Coe in May 1996 might be
a candidate for glider synthesis. Initial attempts to construct a
synthesis for this spaceship got fairly close, but it was only in
March 2003 that Summers and Elkies managed to find a way to perform
the crucial last step. Summers then used the new synthesis to build
a c/2 forward rake for the 2c/5 spaceship; this was the first example
in Life of a rake which fires spaceships that travel in the same
direction as the rake but more slowly.
A 3-glider synthesis of a pentadecathlon is shown in the diagram
below. This was found in April 1997 by Heinrich Koenig and came as a
surprise, as it was widely assumed that anything using just three
gliders would already be known.

glider to 2 blocks
A converter discovered by Sergei Petrov on 8
October 2011, used in his later G4 receiver.

glider to block
A converter discovered by Sergei Petrov that places
a block at its right edge in response to a single glider input.
This has a variety of uses in Herschel circuitry and other
signal-processing applications.

glider train
A certain p64 c/2 orthogonal puffer that produces two
rows of blocks and two backward glider waves. Ten of these were
used to make the first breeder.

glide symmetric
Undergoing simultaneous reflection and translation. A
glide symmetric spaceship is sometimes called a flipper.
Gn
An abbreviation specific to converters that produce multiple
gliders. A "G" followed by any integer value means that the
converter produces a tandem glider - two parallel glider outputs
with lanes separated by the specified number of half diagonals.
Golly
A cross-platform open source Life program by Andrew Trevorrow
and Tomas Rokicki. Unlike most Life programs it includes the ability
to run patterns using the hashlife algorithm. It is available from
http://golly.sourceforge.net.
Gosper glider gun
The first known gun, and indeed the first known
finite pattern displaying infinite growth, found by Bill Gosper in
November 1970. This period 30 gun remains the smallest known gun in
terms of its bounding box, though some variants of the p120
Simkin glider gun have a lower population. Gosper later constructed
several other guns, such as new gun and the p144 gun shown under
factory. See also p30 gun.
grammar
A set of rules for connecting components together to make
an object such as a spaceship, oscillator or still life. For
example, in August 1989 Dean Hickerson found a grammar for
constructing an infinite number of short wide c/3 period 3
spaceships, using 33 different components and a table showing the
ways that they can be joined together.
grandfatherless
A traditional name for a pattern with one or more
parents but no grandparent. This was a hypothetical designation
until May 2016. See grandparent for details.
grandparent
A pattern is said to be a grandparent of the pattern it
gives rise to after two generations. For over thirty years, a
well-known open problem was the question of whether any pattern
existed that had a parent but no grandparent. In 1972, LifeLine
Volume 6 mentioned John Conway's offer of a $50 prize for a solution
to the problem, but it remained open until May 2016 when a user with
the conwaylife.com forum handle 'mtve' posted an example.
Other patterns have since been found that have a grandparent but no
great-grandparent, or a great-grandparent but no
great-great-grandparent. Further examples in this series almost
certainly exist, but as of July 2018 none have yet been found.
Gray counter
p4
Found in 1971. If you look at this in the right
way you will see that it cycles through the Gray codes from 0 to 3.
Compare with R2D2.

great on-off
p2

grey counter
= Gray counter (This form is erroneous, as Gray is
surname, not a colour.)
grow-by-one object
A pattern whose population increases by one cell
every generation. The smallest known grow-by-one object is the
following 44-cell pattern (David Bell's one-cell improvement of a
pattern found by Nicolay Beluchenko, September 2005).

growing/shrinking line ship
A line ship in which the line
repeatedly grows and shrinks, resulting in a high-period spaceship.
growing spaceship
An object that moves like a spaceship, except
that its front part moves faster than its back part and a wick
extends between the two. Put another way, a growing spaceship is a
puffer whose output is burning cleanly at a slower rate than the
puffer is producing it. Examples include blinker ships,
pi ships, and some wavestretchers.
gunstar
Any of a series of glider guns of period 144+72n (for all
non-negative integers n) constructed by Dave Buckingham in 1990 based
on his transparent block reaction and Robert Wainwright's p72
oscillator (shown under factory).
gutter
A single straight line of cells along the axis of symmetry of
a mirror-symmetric pattern. Most commonly this is an orthogonal
line, and the pattern is then odd-symmetric (as opposed to
even-symmetric, where the axis of symmetry follows the boundary
between two rows or columns of cells).
The birth rule for Conway's Life trivially implies that if there
are no live cells in the gutter of a symmetric pattern, new cells can
never be born there. For examples, see 44P5H2V0, 60P5H2V0,
Achim's p4, brain, c/6 spaceship, centinal, p54 shuttle,
pufferfish, snail, spider, and pulsar (in two orientations).
half-baked knightship
(6,3)c/2621440, p2621440
A self-supporting
macro-spaceship with adjustable period but fixed direction, based
on the half-bakery reaction. This was the first spaceship based on
this reaction, constructed in December 2014 by Adam P. Goucher. It
moves 6 cells horizontally and 3 cells vertically every 2621440+8N
ticks, depending on the relative spacing of the two halves. It is
one of the slowest known knightships, and the first one that was
not a Geminoid. Chris Cain optimized the design a few days later to
create the Parallel HBK.
The spaceship produces gliders from near-diagonal lines of
half-bakeries, which collide with each other at 180 degrees. These
collisions produce monochromatic salvos that gradually build and
trigger seeds, which in turn eventually construct small
synchronized salvos of gliders. These re-activate the lines of
half-bakeries, thus closing the cycle and moving the entire spaceship
obliquely by (6,3).
half-bakery reaction
The key reaction used in the
half-baked knightship and Parallel HBK, where a half-bakery is
moved by (6,3) when a glider collides with it, and the glider
continues on a new lane. Ivan Fomichev noticed in May 2014 that
pairs of these reactions at the correct relative spacing can create
90-degree output gliders:

Halfmax
A pattern that acts as a spacefiller in half of the Life
plane, found by Jason Summers in May 2005. It expands in three
directions at c/2, producing a triangular region that grows to fill
half the plane.
hammer
To hammer a LWSS, MWSS or HWSS is to smash things into
the rear end of it in order to transform it into a different type of
spaceship. A hammer is the object used to do the hammering. In the
following example by Dieter Leithner an LWSS is hammered by two more
LWSS to make it into an MWSS.

hammerhead
A certain front end for c/2 spaceships. The central
part of the hammerhead pattern is supported between two MWSS. The
picture below shows a small example of a spaceship with a
hammerhead front end (the front 9 columns).

harbor
p5
Found by Dave Buckingham in September 1978. The name is
by Dean Hickerson.

harvester
c p4 fuse
Found by David Poyner, this was the first
published example of a fuse. The name refers to the fact that it
produces debris in the form of blocks which contain the same number
of cells as the fuse has burnt up.
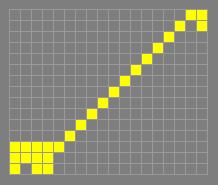
hashlife
A Life algorithm by Bill Gosper that is designed to take
advantage of the considerable amount of repetitive behaviour in many
large patterns of interest. It provides a means of evolving
repetitive patterns millions (or even billions or trillions) of
generations further than normal Life algorithms can manage in a
reasonable amount of time.
The hashlife algorithm is described by Gosper in his paper listed
in the bibliography at the end of this lexicon. Roughly speaking,
the idea is to store subpatterns in a hash table so that the results
of their evolution do not need to be recomputed if they arise again
at some other place or time in the evolution of the full pattern.
This does, however, mean that complex patterns can require
substantial amounts of memory.
Tomas Rokicki and Andrew Trevorrow implemented Hashlife into
Golly in 2005. See also macrocell.
hd
Abbreviation for half diagonal. This metric is used primarily
for relative measurements of glider lanes, often in relation to
self-constructing circuitry; compare Gn.
heat
For an oscillator or spaceship, the average number of cells
which change state in each generation. For example, the heat of a
glider is 4, because 2 cells are born and 2 die every generation.
For a period n oscillator with an r-cell rotor the heat is at
least 2r/n and no more than r(1-(n mod 2)/n). For n=2 and n=3 these
bounds are equal.
heavyweight spaceship
= HWSS
hebdarole
p7
Found by Noam Elkies, November 1997. Compare
fumarole. The smaller version shown below was found soon after by
Alan Hensel using a component found by Dave Buckingham in June 1977.
The top ten rows can be stabilized by their mirror image (giving an
inductor) and this was the original form found by Elkies.

hectic
p30
Found by Robert Wainwright in September 1984.

Heisenburp device
A pattern which can detect the passage of a
glider without affecting the glider's path or timing. The first
such device was constructed by David Bell in December 1992. The
term, coined by Bill Gosper, refers to the fact that Heisenberg's
Uncertainty Principle fails to apply in the Life universe. See also
stable pseudo-Heisenburp and natural Heisenburp.
The following is an example of the kind of reaction used at the
heart of a Heisenburp device. The glider at bottom right alters the
reaction of the other two gliders without itself being affected in
any way.

helix
A convoy of standard spaceships used in a Caterpillar to
move some piece of debris at the speed of the Caterpillar. The
following diagram illustrates the idea. The leading edge of this
example helix, represented by the glider at the upper right in the
pattern below, moves at a speed of 65c/213, or slightly faster than
c/4.

Adjustable-speed helices can produce a very wide range of spaceship
speeds; see Caterloopillar.
Herschel
stabilizes at time 128
The following pattern which occurs
at generation 20 of the B-heptomino.

The name is commonly ascribed to the Herschel heptomino's
similarity to a planetary symbol. William Herschel discovered Uranus
in 1781. However, in point of fact a Herschel bears no particular
resemblance to either of the symbols used for Uranus, but does
closely resemble the symbol for Saturn. So the appropriate name might
actually be "Huygens", but "Herschel" is now universally used by
tradition.
Herschels are one of the most versatile types of signal in stable
circuitry. R-pentominoes and B-heptominoes naturally evolve into
Herschels, and converters have also been found that change
pi-heptominoes and several other signal types into Herschels, and
vice versa. See elementary conduit.
Herschel circuit
A series of Herschel conduits or other components,
connected by placing them so that the output Herschels from early
conduits become the input Herschels for later conduits. Often the
initial component is a converter accepting some other signal type
as input - usually a glider, in which case a syringe is most
commonly used. The Silver reflector is a well-known early
Spartan Herschel circuit from before the syringe was discovered,
where the initial converter is a Callahan G-to-H.
Sometimes a direct connection between two conduits is not possible
due to unwanted gliders that destroy required catalysts, or wanted
gliders that are not able to escape. In this case, small "spacer"
conduits such as F116, F117, Fx77, R64, L112, or L156 can
be inserted between the other conduits to solve the problem.
Some converter or factory conduits do not produce a Herschel as
output, instead generating other useful results such as gliders,
boats or MWSSes. See Herschel-to-glider, demultiplexer, and
H-to-MWSS respectively for examples of these. For those conduits
which do produce an unwanted Herschel, an eater such as SW-2 can
be added to delete it.
If the first and last conduits of a chain connect to each other in
a loop then there is no need for a syringe to generate the first
Herschel, or an eater to consume the last one. The circuit becomes a
self-supporting Herschel loop. A loop is also formed by a
syringe connected to a Herschel-to-glider converter, with the
glider reflected back to the syringe's input with glider reflectors
of the appropriate colour, usually Snarks. In either case, if the
loop has a surplus glider output, it becomes a gun; if no output
is available it is an emu.
Herschel conduit
A conduit that moves a Herschel from one place
to another. See also Herschel loop.
Well over a hundred simple stable Herschel conduits are currently
known. As of June 2018 the number is approximately 150, depending on
the precise definition of "simple" - e.g., fitting inside a 100×100
bounding box, and producing output in no more than 300 ticks. In
general a Herschel conduit can be called "simple" if its active
reaction does not return to a Herschel stage except at its output.
Compare elementary conduit, composite conduit. A description of
common usage in complex circuitry, using syringes and Snarks to
make compact connections, can be found in Herschel circuit.
The original universal set consisted of sixteen stable Herschel
conduits, discovered between 1995 and 1998 by Dave Buckingham (DJB)
and Paul Callahan (PBC). These are shown in the following table. In
this table, the number in "name/steps" is the number of ticks
needed to produce an output Herschel from the input Herschel. "m"
tells how the Herschel is moved (R = turned right, L = turned left, B
= turned back, F = unturned, f = flipped), and "dx" and "dy" give the
displacement of the centre cell of the Herschel (assumed to start in
the orientation shown above).
-----------------------------------------
name/steps m dx dy discovery
-----------------------------------------
R64 R 11 9 DJB, Sep 1995
Fx77 Fflip 25 -8 DJB, Aug 1996
L112 L 12 -33 DJB, Jul 1996
F116 F 32 1 PBC, Feb 1997
F117 F 40 -6 DJB, Jul 1996
Bx125 Bflip -9 -17 PBC, Nov 1998
Fx119 Fflip 20 14 DJB, Sep 1996
Fx153 Fflip 48 -4 PBC, Feb 1997
L156 L 17 -41 DJB, Aug 1996
Fx158 Fflip 27 -5 DJB, Jul 1996
F166 F 49 3 PBC, May 1997
Fx176 Fflip 45 0 PBC, Oct 1997
R190 R 24 16 DJB, Jul 1996
Lx200 Lflip 17 -40 PBC, Jun 1997
Rx202 Rflip 7 32 DJB, May 1997
Bx222 Bflip -6 -16 PBC, Oct 1998
-----------------------------------------
See also Herschel transceiver.
Herschel descendant
A common active pattern occurring at generation
22 of a Herschel's evolution:

There are other evolutionary paths leading to the same pattern,
including the modification of a B-heptomino implied by generation
21 of a Herschel.
Herschel great-grandparent
A specific three-tick predecessor of a
Herschel, commonly seen in Herschel conduit collections that
contain dependent conduits. In some situations it is helpful to
display the input reaction in this form instead of the standard
Herschel form.

Dependent conduit inputs are catalysed by a transparent block
before the Herschel's standard form can appear, and before the
Herschel's first natural glider is produced. This means that these
conduits will fail if an actual Herschel is placed in the "correct"
input location for a dependent conduit. Refer to F166 or Lx200
to see the correct relative placement of the standard transparent
block catalyst.
Almost all known Herschel conduits produce a Herschel
great-grandparent near the end of their evolutionary sequence. In
the original universal set of Herschel conduits, Fx158 is the
only exception.
Herschel loop
A cyclic Herschel track. Although no loop of length
less than 120 generations has been constructed it is possible to make
oscillators of smaller periods by putting more than one Herschel in
a higher-period track. In this way oscillators, and in most cases
guns, of all periods from 54 onwards can now be constructed
(although the p55 case is a bit strange, shooting itself with gliders
in order to stabilize itself). A mechanism for a period-52 loop was
found in April 2018, but it includes a stage where the signal is
carried by a triplet of gliders so it may not be considered to be a
pure Herschel loop. The missing period, 53, is a difficult case
simply because 53 is prime and so no small sparkers or reflectors are
available.
See Simkin glider gun and p256 gun for the smallest known
Herschel loops. See also emu and omniperiodic.
Herschel receiver
Any circuit that converts a tandem glider into
a Herschel signal. The following diagram shows a pattern found
by Paul Callahan in 1996, as part of the first stable glider
reflector. Used as a receiver, it converts two parallel input
gliders (with path separations of 2, 5, or 6) to an R-pentomino.
The signal is then converted to a Herschel by one of several known
mechanisms, the first of which was found by Dave Buckingham way back
in 1972. The second is elementary conduit RF48H, found by
Stephen Silver in October 1997. The receiver version shown below
uses Buckingham's R-to-Herschel converter, which is made up of
elementary conduit RF28B followed by BFx59H.

Herschel stopper
A method of cleanly suppressing a Herschel signal
with an asynchronous boat-bit, discovered by Dean Hickerson.
Here a ghost Herschel marks the location of the output signal, in
cases where the boat-bit is not present. Other boat-bit locations
that allow for clean suppression of a Herschel are also known.

This term is also sometimes used to refer to any mechanism that
cleanly suppresses a Herschel. These usually allow the Herschel's
first natural glider to escape, so they are more commonly
classified as converters. See SW-2.
Herschel-to-glider
The largest category of elementary conduit.
Gliders are very common and self-supporting, so it's much easier to
find these than any other type of output signal. A large
collection of these H-to-G converters has been compiled, with many
different output lanes and timings. These can be used to
synchronize multiple signals to produce gun patterns or complex
logic circuitry. See NW31T120 for an example.
Herschel transmitter
Any Herschel-to-two-glider converter that
produces a tandem glider that can be used as input to a
Herschel receiver. If the gliders are far enough apart, and if one
of the gliders is used only for cleanup, then the transmitter is
ambidextrous: with a small modification to the receiver, a
suitably oriented mirror image of the receiver will also work.
The following diagram shows a stable Herschel transmitter found
by Paul Callahan in May 1997:

Examples of small reversible p6 and p7 transmitters are also known,
and more recently several alternate Herschel transceivers have been
found with different lane spacing, e.g., 0, 2, 4, 6, and 13.
Hertz oscillator
p8
Compare negentropy, and also cauldron.
Found by Conway's group in 1970.

HFx58B
A common Herschel to B-heptomino converter, used as the
first stage of F117 and many other Herschel conduits. There are
two variants, both shown in the pattern below.

H-heptomino
Name given by Conway to the following heptomino. After
one generation this is the same as the I-heptomino.

high-bandwidth telegraph
p960, p30 circuitry
A variant of the
telegraph constructed by Louis-François Handfield in February 2017,
using periodic components to achieve a transmission rate of one bit
per 192 ticks. The same ten signals are sent as in the original
telegraph and the p1 telegraph, but information is encoded more
efficiently in the timing of those signals. Specifically, the new
transmitter sends five bits every 960 ticks by adjusting the relative
timings inside each of the five mirror-image paired subunits of the
composite signal in the beehive-chain lightspeed wire fuse.
highway robber
Any mechanism that can retrieve a signal from a
spaceship lane while allowing spaceships on nearby lanes to pass by
unaffected. In practice the spaceship is generally a glider. The
signal is removed from the lane, an output signal is generated
elsewhere, and the highway robber returns to its original state. A
competent highway robber does not affect gliders even on the lane
adjacent to the affected glider stream, except during its recovery
period.
A perfect highway robber doesn't affect later gliders even in the
lane to which it is attached, even during its recovery period. Below
is a near-perfect highway robber "bait" that requires three
synchronized signals to rebuild (the Herschel, B-heptomino, and
glider.) The glider at the top right passes by unharmed, but
another glider following on the same lane 200 ticks later will be
cleanly reflected to a new path, and another glider following that
one will also pass by unharmed. The only imperfection is a few ticks
at the very end of the reconstruction, as the beehive is being
rebuilt:

hivenudger
c/2 orthogonally, p4
A spaceship found by Hartmut
Holzwart in July 1992. (The name is due to Bill Gosper.) It
consists of a pre-beehive escorted by four LWSS. In fact any
LWSS can be replaced by a MWSS or an HWSS, so that there are 45
different single-hive hivenudgers.
.png)
Wider versions can be made by stabilizing the front of the extended
"pre-beehive", as in the line puffer shown below.
.png)
honey bit
A block and pond constellation used in the
OTCA metapixel by Brice Due in 2006, to store and retrieve a bit of
data - specifically, the presence or absence of a neighbor
metacell. The "0" state of the honey bit memory unit is a simple
beehive, which is also the source of the name.
An input glider collides with the beehive to convert it into the
honey bit constellation, which can be thought of as a value of "1"
stored in the memory unit. A passing LWSS can then test for the
presence of the pond. If a collision occurs, the LWSS and the honey
bit constellation are mutually annihilated, leaving just the original
beehive. Below is the honeybit constellation with the two reactions
occurring in the opposite order - test, then reset.
.png)
If the pond is not present, the LWSS passes by the beehive without
affecting it. Thus a test input has an output for the "0" case, but
not for the "1" case. For an alternative memory-unit mechanism with
both "0" and "1" outputs, see demultiplexer.
The honey bit is also an interesting eater for the HWSS as
shown below. An HWSS colliding with the pond happens to create the
exact same reset glider used in the above memory unit.
.png)
honeycomb
p1

honey farm
p1
A common formation of four beehives.

hook
Another term for a bookend. It is also used for other
hook-shaped things, such as occur in the eater1 and the
hook with tail, for example.
hook with tail
p1
For a long time this was the smallest
still life without a well-established name. It is now a vital
component of the smallest known HWSS gun, where it acts as a
rock.

houndstooth agar
The p2 agar that results from tiling the plane
with the following pattern.

H-to-MWSS
A Spartan converter found by Tanner Jacobi in October
2015, which converts an input Herschel to a middleweight spaceship.
The key discovery was a very small but slightly dirty H-to-MWSS
conduit, where a Herschel is catalyzed to produce an MWSS but also
leaves behind a beehive. Prefixing two R64 conduits to this
produces a composite converter that successfully deletes the
beehive in advance, using the input Herschel's
first natural glider.

There are many other ways to remove the beehive using a spare glider
or additional conduits, but they are generally less compact than
this.
hustler
p3
Found by Robert Wainwright, June 1971.

hustler II
p4

HW emulator
p4
Found by Robert Wainwright in June 1980. See also
emulator.
HWSS
c/2 orthogonally, p4
A heavyweight spaceship, the fourth most
common spaceship. Found by Conway in 1970 by modifying a LWSS.
See also MWSS.
.png)
The HWSS possesses both a tail spark and a domino belly spark
which can easily perturb other objects as it passes by. The
spaceship can also perturb some objects in additional ways. For
examples, see puffer and glider turner.
Dave Buckingham found that the HWSS can be synthesized using three
gliders as shown below:
.png)
HW volcano
p5
A p5 domino sparker, found by Dean Hickerson in
February 1995.

At least four progressively smaller forms of this sparker have been
found, including a 25-cell-wide version found by David Eppstein in
2003, and a vertically narrower 28-cell-wide version by Karel Suhajda
in 2004. Scot Ellison's 17-cell-wide version is shown in the
zweiback entry.
I-heptomino
Name given by Conway to the following heptomino. After
one generation this is the same as the H-heptomino.

Immigration
A form of colourised Life in which there are two types
of ON cell, a newly-born cell taking the type of the majority of its
three parent cells and surviving cells remaining of the same type
as in the previous generation.
inductor
Any oscillator with a row of dead cells down the middle
and whose two halves are mirror images of one another, both halves
being required for the oscillator to work. The classic examples are
the pulsar and the tumbler. If still lifes are considered as p1
oscillators then there are numerous simple examples that include this
kind of central gutter, such as table on table, dead spark coil
and cis-mirrored R-bee. Some spaceships, such as the brain, the
snail and the spider, use the same principle.
infinite glider hotel
A pattern by David Bell, named after Hilbert's
"infinite hotel" scenario in which a hotel with an infinite number of
rooms has room for more guests even if it is already full, simply by
shuffling the old guests around.
In this pattern, two pairs of Corderships moving at c/12 are
pulling apart such that there is an ever-lengthening glider track
between them. Every 128 generations another glider is injected
into the glider track (see LWSS-glider bounce), joining the gliders
already circulating there. The number of gliders in the track
therefore increases without limit.
The tricky part of this construction is that even though all the
previously injected gliders are repeatedly flying through the
injection point, that point is guaranteed to be empty when it is time
for the next glider to be injected.
infinite growth
Growth of a finite pattern such that the population
tends to infinity, or at least is unbounded. Sometimes the term is
used for growth of something other than population (for example,
length), but here we will only consider infinite population growth.
The first known pattern with infinite growth in this sense was the
Gosper glider gun, created in a response to a $50 prize challenge
by John Conway. Martin Gardner's October 1970 article described the
challenge as "Conway conjectures that no pattern can grow without
limit", but Conway later explained that he had always expected that
this would be disproved. The original purpose in investigating CA
rules including B3/S23 was to show that a very simple two-state rule
could support a universal computer and/or universal constructor.
If all finite patterns could be proven to be bounded, neither of
these would be possible.
An interesting question is: What is the minimum population of a
pattern that exhibits infinite growth? In 1971 Charles Corderman
found that a switch engine could be stabilized by a pre-block in
a number of different ways, giving 11-cell patterns with infinite
growth. This record stood for more than quarter of a century until
Paul Callahan found, in November 1997, two 10-cell patterns with
infinite growth. The following month he found the one shown below,
which is much neater, being a single cluster. This produces a
stabilized switch engine of the block-laying type.
.png)
Nick Gotts and Paul Callahan showed in October 1997 that there is no
infinite growth pattern with fewer than 10 cells, so that question
has now been answered.
In October 2014, Michael Simkin discovered a three-glider collision
that produces a glider-producing stabilized switch engine and thus
produces infinite growth from the smallest possible number of gliders
(since all 71 2-glider collisions have a finite limit population).
Also of interest is the following pattern (again found by
Callahan), which is the only 5×5 pattern with infinite growth. This
too emits a block-laying switch engine.
.png)
Following a conjecture of Nick Gotts, Stephen Silver produced, in
May 1998, a pattern of width 1 which exhibits infinite growth. This
pattern was very large (12470×1 in the first version, reduced to
5447×1 the following day). In October 1998 Paul Callahan did an
exhaustive search, finding the smallest example, the 39×1 pattern
shown below. This produces two block-laying switch engines,
stability being achieved at generation 1483.
.png)
Larger patterns have since been constructed that display
quadratic growth.
Although the simplest infinite growth patterns grow at a rate that
is (asymptotically) linear, many other types of growth rate are
possible, quadratic growth (see also breeder) being the fastest.
Dean Hickerson has found many patterns with unusual growth rates,
such as sawtooths and a caber tosser. Another pattern with
superlinear but non-quadratic growth is Gotts dots.
See also Fermat prime calculator.
inject
A reaction in which a hole in a regular spaceship stream is
filled partially or fully by adding a new spaceship of the same type
without affecting the existing spaceships in the stream. Depending
on the period of the stream, different mechanisms can be used. For
adding a spaceship to an existing multi-lane convoy, see
inserter.
For large period glider streams, simple reactions such as
LWSS-LWSS bounce and LWSS-glider bounce suffice. If Herschel
technology is used, a large number of edge shooters and
transparent conduits are known. Simple examples include the NW31
Herschel-to-glider converter and the Fx119 inserter.
Shown below is an injector found by Dave Buckingham that can fill a
hole in a p15 glider stream:

For very low-period glider streams, a GIG is a much more efficient
insertion method, in the sense that fewer synchronized signals
are needed. However, it has been shown that colliding gliders can
complete an insertion even into a single-glider gap in a period-14
stream.
inline inverter
The following reaction in which a p30 gun can be
used to invert the presence or absence of gliders in a p30 stream,
with the output glider stream being in the same direction as the
input glider stream.

inserter
A mechanism that can add another spaceship into a stream or
convoy of other spaceships without affecting the existing spaceships.
For examples see Fx119 inserter, tee, GIG, clock insertion
and inject.
integral sign
p1

interchange
p2
A common formation of six blinkers.

intermediate target
A temporary product of a partial slow salvo,
elbow operation, or glider synthesis. An intermediate target is
a useful step toward a desired outcome, but will not appear in the
final construction.
intermittent stream
A stream of spaceships which is based on a
periodic stream, but which can contain holes where some of the
spaceships are not present. There is a base period for the
intermittent stream such that if a spaceship arrives at a specific
location, then it always does so at a generation which is a multiple
of the base period. For example, the output from a period 30 glider
gun where every third glider is deleted is an intermittent stream. A
pseudo-random glider generator can produce a complicated
intermittent stream with no obvious pattern.
Intermittent streams can be used to transmit signals, where holes
in the stream can also convey information. For example, the stream
can be processed by an inverter having the same period.
intermitting glider gun
Despite the name, an intermitting glider gun
(IMG) is more often an oscillator than a gun. There are two
basic types. A type 1 IMG consists of two guns firing at one another
in such a way that each gun is temporarily disabled on being hit by a
glider from the other gun. A type 2 IMG consists of a single gun
firing at a 180-degree glider reflector in such a way that
returning gliders temporarily disable the gun.
Both types of IMG can be used to make glider guns of periods that
are multiples of the base period. This is done by firing another gun
across the two-way intermittent stream of gliders in the IMG in
such a way that gliders only occasionally escape.
inverter
A device which can be used to invert the presence or absence
of spaceships in an intermittent stream of spaceships. The device
must be a gun whose period matches the base period of the stream,
since if there are no input spaceships then the device must produce
spaceships as the result of the inversion. Typically the spaceships
are gliders, and the inverter is made from a glider gun. Inverters
provide a way to produce a NOT logic operation on a stream.
There are several ways to produce an inverter. The simplest method
is to simply hit the output of a gun with the input stream to delete
its spaceships, producing an output stream that is always turned 90
degrees from the input stream. An example is the northernmost p30
gun in the glider duplicator example pattern. For one way to
produce an inverted output stream which is not turned, see
inline inverter.
Iwona
stabilizes at time 28786
The following methuselah found by
Andrzej Okrasinski in August 2004.
It has a final population of 3091 and covers an area of 413 by 364
cells, not counting the 47 gliders it produces. Its ash consists
of typical stable objects and blinkers, along with the relatively
rare paperclip.
jack
p4
Found by Robert Wainwright, April 1984.
jagged lines
A pattern constructed by Dean Hickerson in May 2005 that
uses puffers to produce a line of bi-blocks that weaves back and
forth in a complicated way.
jam
p3
Found by Achim Flammenkamp in 1988, but not widely known
about until its independent discovery (and naming) by Dean Hickerson
in September 1989. Compare with mold. In fact this is really very
like caterer. In terms of its 7×7 bounding box it ties with
trice tongs as the smallest p3 oscillator.

Jaws
A breeder constructed by Nick Gotts in February 1997. In the
original version Jaws had an initial population of 150, which at
the time was the smallest for any known pattern with
superlinear growth. In November 1997 Gotts produced a 130-cell
Jaws using some switch engine predecessors found by Paul
Callahan. See switch-engine ping-pong for the lowest-population
superlinear growth pattern as of July 2018, along with a list of the
record-holders.
Jaws consists of eight pairs of switch engines which produce a new
block-laying switch engine (plus masses of junk) every 10752
generations. It is therefore an MMS breeder.
JHC
John Horton Conway. Also another name for monogram.
Jolson
p15
Two blocks hassled by two pentadecathlons. Found
by Robert Wainwright in November 1984 and named by Bill Gosper. A p9
version using snackers instead of pentadecathlons is also possible.

Justyna
stabilizes at time 26458
The following methuselah found
by Andrzej Okrasinski in May 2004.

Karel's p15
p15
An oscillator discovered by Karel Suhajda on
December 11, 2002. It consists of a period 15 rotor supported by the
domino spark of a pentadecathlon. It provides accessible sparks that
can be used to perturb reactions or thin signal streams.

keeper
A type of factory circuit that always results in the
presence of an object in the output location, whether or not the
object was previously present. In many cases it is easy to construct
examples by connecting multiple circuits to shoot down an object with
a glider, then rebuild the object again later. The smallest keeper
circuits accomplish the same thing more directly with a lucky
preliminary spark from the active reaction, which removes the
existing object (if any) just before the construction occurs. Below
is a useful block keeper with a Herschel input.

kickback reaction
The following collision of two gliders whose
product is a single glider travelling in the opposite direction to
one of the original gliders. This is important in the proof of the
existence of a universal constructor, and in Bill Gosper's
total aperiodic, as well as a number of other constructions.
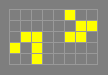
See also 180-degree kickback.
Klein bottle
As an alternative to a torus, it's possible to make a
finite Life universe in the form of a Klein bottle. The simplest way
to do this is to use an m × n rectangle with the top edge joined to
the bottom edge (as for a torus) and the left edge twisted and joined
to the right.
knightship
2m,m
/n - that is, a spaceship of
any speed that moves obliquely in a (2,1) direction. The first
Conway's Life knightship was a variant of Andrew Wade's Gemini
spaceship, constructed in May 2010. The next was an even slower
knightship based on the half-bakery reaction.
A knightship must be asymmetric and its period must be at least 6.
This is barely within the range of current search programs, as
proven by the discovery on March 6, 2018 of an elementary
knightship, Sir Robin, by Adam P. Goucher and Tomas Rokicki.
By analogy with the corresponding fairy chess pieces, spaceships of
types (3m,m)/n, (3m,2m)/n and (4m,m)/n would presumably be called
camelships, zebraships and giraffeships, respectively. Such
spaceships do exist (see universal constructor) but small
elementary versions are even more difficult to search for. Any of
these ship types could be constructed by trivially modifying a Gemini
spaceship, or less trivially by reprogramming one of the more recent
small Geminoid construction arms, but as of July 2018 a camelship
Gemini is the only example that has been explicitly built.
Alternatively, the term "knightship" is regularly used to refer to
any oblique spaceship, such as the original Gemini or the
waterbear.
L156
A composite conduit, one of the original sixteen
Herschel conduits, discovered by Dave Buckingham in August 1996.
It is made up of three elementary conduits, HLx69R + RF28B +
BFx59H. After 156 ticks, it produces a Herschel turned 90
degrees counterclockwise at (17, -41) relative to the input. Its
recovery time is 62 ticks. It can be made Spartan by replacing
the snake with an eater1 in one of two orientations. Additional
gliders can be produced by removing the southeasternmost eater, or by
replacing the RF28B elementary conduit by an alternate version. A
ghost Herschel in the pattern below marks the output location:

lake
p1
Any still life consisting of a simple closed curve made
from diagonally connected dominoes. The smallest example is the
pond, and the next smallest is this (to which the term is sometimes
restricted):

lane
A path traveled by a glider, or less commonly a spaceship such
as a loafer. The lane is centered on the line of symmetry (if any)
of the spaceship in question. If a lane is clear, then the spaceship
can travel along it without colliding or interfering with any other
objects.
Diagonal lanes are often numbered consecutively, in half-diagonals
(hd). Occasionally diagonal lane measurements are given in
quarter-diagonals (qd), in part because diagonally symmetric
spaceships have a line of symmetry 1qd away from the lines available
for gliders. It's also convenient that moving a glider forward by
100qd (for example) has the same effect as evolving the same glider
for 100 ticks.
Laputa
p2
Found by Rich Schroeppel, September 1992.

large prime oscillator
Any oscillator with a relatively small
bounding box whose period is a very large prime. (If the
bounding-box restriction is removed, then eight gliders travelling in
a four-Snark loop would provide a trivial example for any chosen
prime.) The first such oscillator was built by Gabriel Nivasch in
2003. The current record holder is an oscillator constructed by Adam
P. Goucher with a period that is a Mersenne prime with 13,395 digits
(244497-1).
The next higher Mersenne-prime oscillator, period 286243-1, could
be constructed with quadri-Snarks and semi-Snarks. It would
actually be significantly smaller than the current record holder. As
of June 2018 the construction of this pattern has not yet been
completed.
Lidka
stabilizes at time 29053
A methuselah found by Andrzej
Okrasinski in July 2005.
.png)
The following variant, pointed out by David Bell, has two fewer cells
and lasts two generations longer.
.png)
Life
A 2-dimensional 2-state cellular automaton discovered by John
Conway in 1970. The states are referred to as ON and OFF (or live
and dead). The transition rule is as follows: a cell that is ON will
remain ON in the next generation if and only if exactly 2 or 3 of the
8 adjacent cells are also ON, and a cell that is OFF will turn ON if
and only if exactly 3 of the 8 adjacent cells are ON. (This is more
succinctly stated as: "If 2 of your 8 nearest neighbours are ON,
don't change. If 3 are ON, turn ON. Otherwise, turn OFF.")
LifeHistory
A multistate CA rule supported by Golly, equivalent to
two-state B3/S23 Life but with several additional states intended for
annotation purposes. A "history" state records whether an off cell
has ever turned on in the past, and other states allow on and off
cells to be permanently or temporarily marked, without affecting the
evolution of the pattern.
LifeLine
A newsletter edited by Robert Wainwright from 1971 to 1973.
During this period it was the main forum for discussions about Life.
The newsletter was nominally quarterly, but the actual dates of its
eleven issues were as follows:
Mar, Jun, Sep, Dec 1971
Sep, Oct, Nov, Dec 1972
Mar, Jun, Sep 1973
Lifenthusiast
A Life enthusiast. Term coined by Robert Wainwright.
lifesrc
David Bell's Life search program for finding new
spaceships and oscillators. This is a C implementation of an
algorithm developed by Dean Hickerson in 6502 assembler.
Although lifesrc itself is a command-line program, Jason Summers
has made a GUI version called WinLifeSearch for Microsoft Windows.
A Java version, JavaLifeSearch, was written in November 2012 by
Karel Suhajda.
The lifesrc algorithm is only useful for very small periods, as the
amount of computing power required rises rapidly with increasing
period. For most purposes, period 7 is the practical limit with
current hardware.
Lifesrc is available from http://tip.net.au/~dbell/ (source code
only). Compare gfind.
LifeViewer
A scriptable Javascript Life pattern viewer written by
Chris Rowett, used primarily on the conwaylife.com discussion forums.
light bulb
p2
Found in 1971.
.png)
The same rotor can be embedded in a slightly smaller stator like
this:
.png)
lightspeed bubble
A type of negative spaceship travelling through
the zebra stripes agar. The center of the bubble is simple empty
space, and the length and/or width of the bubble can usually be
extended to any desired size.
Below is a small stabilized section of agar containing a sample
lightspeed bubble, found by Gabriel Nivasch in August 1999. The
bubble travels to the left at the speed of light, so it will
eventually reach the edge of any finite patch and destroy itself and
its supporting agar.
.png)
An open problem related to lightspeed bubbles was whether large
extensible empty areas could be created whose length was not
proportional to the width (as it must be in the above case, due to
the tapering back edge). This was solved in February 2017 by Arie
Paap; a simple period-2 solution is shown below.
.png)
lightspeed wire
Any wick that can burn non-destructively at the
speed of light. Lightspeed wires are a type of reburnable fuse.
These are potentially useful for various things, but so far the
necessary mechanisms are very large and unwieldy. In October 2002,
Jason Summers discovered a lightspeed reaction travelling through an
orthogonal chain of beehives. Summers completed a period-1440
lightspeed telegraph based on this reaction in 2003.
.png)
A stable lightspeed transceiver mechanism using this same
signal reaction, the p1 telegraph, was constructed by Adam P.
Goucher in 2010; the bounding boxes of both the transmitter and
receiver are over 5000 cells on a side. A more compact periodic
high-bandwidth telegraph with a much improved transmission rate was
completed by Louis-François Handfield in 2017.
The following diagram shows an older example of a lightspeed wire,
with a small defect that travels along it at the speed of light. As
of June 2018, no method has been found of creating such a defect in
the upstream end of this particular stable wire, or of
non-destructively detecting the arrival of the defect and repairing
the wire at the downstream end.
.png)
lightweight spaceship
= LWSS
linear propagator
A self-replicating pattern in which each copy of a
pattern produces one child that is an exact copy of itself. The
child pattern then blocks the parent from any further replication.
An example was constructed by Dave Greene on 23 November 2013, with a
construction arm using two glider lanes separated by 9hd. By some
definitions, due to its limited one-dimensional growth pattern, the
linear propagator is not a true replicator. Compare
quadratic replicator.
line crosser
A pattern which is able to send a signal across an
infinite diagonal line of live cells without destroying the line.
David Bell built one in August 2006. It uses many one-shot period
44160 glider guns on both sides of the line having the proper
synchronization to create the reactions shown in
line-cutting reaction and line-mending reaction.
An input glider can arrive at any multiple of 44160 generations to
first cut the line, then send a glider through the gap, and finally
mend the line while leaving an output glider on the other side.
A line crosser whose complete mechanism is on one side of the line
is theoretically possible, using single-channel construction
methods for example.
line-cutting reaction
A reaction that can cut an infinite diagonal
line of cells, leaving a gap with both ends sealed. Such a reaction
is demonstrated below. In actual use the reaction should be spread
out so that the incoming LWSSes don't conflict. See
line-mending reaction for a way to mend the gap.

line-mending reaction
A reaction which can fully mend a sealed gap in
an infinite diagonal line of cells, such as the one produced by a
line-cutting reaction. Such a reaction is demonstrated below. See
the line cutting reaction for a way of creating the gliders
travelling parallel to the line.

This reaction uses spaceships on both sides of the line which need
to be synchronized to each other, for example by passing a glider
through the gap to trigger the creation of the required spaceships
and gliders.
No simple mechanism is known to mend the gap which lies completely
on one side of the line. However, it is technically possible to use
construction arm technology to push objects through the gap to
build and trigger a seed for the required synchronized signals
on the other side.
line puffer
A puffer which produces its output by means of an
orthogonal line of cells at right angles to the direction of travel.
The archetypal line puffer was found by Alan Hensel in March 1994,
based on a spaceship found earlier that month by Hartmut Holzwart.
The following month Holzwart found a way to make extensible c/2
line puffers, and Hensel found a much smaller stabilization the
following day. But in October 1995 Tim Coe discovered that for large
widths these were often unstable, although typically lasting millions
of generations. In May 1996, however, Coe found a way to fix the
instability. The resulting puffers appear to be completely stable
and to exhibit an exponential increase in period as a function of
width, although neither of these things has been proved.
Line puffers have enabled the construction of various difficult
periods for c/2 spaceships and puffers, including occasionally
periods which are not multiples of 4 and which would therefore be
impossible to attain with the usual type of construction based on
standard spaceships. (See frothing puffer for another method of
constructing such periods.) In particular, the first c/2 rake with
period not divisible by 4 was achieved in January 2000 when David
Bell constructed a p42 backrake by means of line puffers.
See also hivenudger and puff suppressor.
linestretcher
A wickstretcher that stretches a single diagonal line
of cells. The first example was constructed by Jason Summers in
March 1999; this was c/12 and used switch engine based puffers
found earlier by Dean Hickerson. The first c/4 example was found by
Hartmut Holzwart in November 2004.
loading dock
p3
Found by Dave Buckingham, September 1972.

loaf
p1

loafer
c/7 orthogonally, p7
A small c/7 spaceship discovered by
Josh Ball on 17 February 2013:
.png)
It has a known 8-glider construction recipe, probably not minimal,
discovered on the following day:
.png)
The loafer was therefore the first new glider-constructible spaceship
in almost a decade. (A glider synthesis for a 2c/5 ship,
60P5H2V0, was found in March 2003.)
loaf pull
The following glider/loaf collision, which pulls a loaf
(3,1) toward the glider source:

loaf siamese barge
p1

lobster
c/7 diagonally, p7
A spaceship discovered by Matthias
Merzenich in August 2011, the first diagonally travelling
c/7 spaceship to be found. It consists of two gliders pulling a
tagalong that then rephases them.

logarithmic growth
A pattern whose population or bounding box
grows no faster than logarithmically, asymptotic to n.log(t) for some
constant n. The first such pattern constructed was the
caber tosser whose population is logarithmic, but whose bounding
box still grows linearly. The first pattern whose bounding box and
population both grow logarithmically was constructed by Jason Summers
with Gabriel Nivasch in 2003. For a pattern with a slower growth
rate than this, see Osqrtlogt.
lone dot agar
An agar in which every live cell is isolated in every
generation. There are many different lone dot agars. All of them
are phoenixes. In 1995 Dean Hickerson and Alan W. Hensel found
stabilizations for finite patches of ten lone dot agars to create
period 2 oscillators. One of these is shown below:

long^3
The next degree of longness after long long. Some people
prefer "extra long".
long^4
The next degree of longness after long^3. Some people
prefer "extra extra long".
long barge
p1

long boat
p1

A long boat can be used as a 90-degree or 180-degree one-time
turner.
long canoe
p1

long integral
p1

long long
The next degree of longness after long. Some people
prefer "very long".
long long barge
p1

long long boat
p1

long long canoe
p1

long long ship
p1

long long snake
p1

long shillelagh
p1

long ship
p1

long snake
p1

loop
p1

lossless elbow
A stationary elbow in a construction arm toolkit
that allows a recipe to turn a corner with no exponential increase
in construction cost. Compare slow elbow. It is theoretically
possible to construct lossless elbows for early construction arms
such as the one in the 10hd Demonoid, but these would currently
have to be very large.
The lossless elbow that has been used the most in practice is the
Snark, which can be constructed directly on a single-channel
construction lane using a Snarkmaker recipe. Controlled
demolition of a Snark is also possible, to remove a temporary elbow
that is no longer needed, and leave a hand target in its place if
necessary for further construction.
A Silver reflector was used as a lossless elbow in the first
spiral growth pattern, attached to a separate
universal constructor component.
lumps of muck
The common evolutionary sequence that ends in the
blockade. The name is sometimes used of the blockade itself, and
can in general be used of any stage of the evolution of the
stairstep hexomino.
LW emulator
p4) The smallest (and least useful
emulator, found by
Robert Wainwright in June 1980.

LWSS
c/2 orthogonally, p4
A lightweight spaceship, the smallest
known orthogonally moving spaceship, and the second most common
(after the glider). Found by Conway when one formed from a random
soup in 1970. See also MWSS and HWSS.
.png)
The LWSS possesses a tail spark which can easily perturb other
objects which grow into its path. The spaceship can also perturb
some objects in additional ways. For examples, see blinker ship,
hivenudger, and puffer train.
Dave Buckingham found that the LWSS can be synthesized in several
different ways using three gliders, and can be constructed from two
gliders and another small object in several more ways. Here is the
fastest synthesis:
.png)
LWSS-glider bounce
The following reaction in which a LWSS and a
glider collide to form a glider heading back between the two input
paths:

This is one way to inject a glider into a existing glider stream.
The infinite glider hotel uses this reaction.
LWSS-LWSS deflection
The following symmetric reaction in which two
LWSSs collide nearly head-on to form two gliders heading apart at 180
degrees from each other. Compare LWSS-LWSS bounce.

LWTDS
Life Worker Time Deficiency Syndrome. Term coined by Dieter
Leithner to describe the problem of having to divide scarce time
between Life and real life.
macrocell
A format used by Golly and its hashlife algorithm,
capable of storing repetitive patterns very efficiently, even if they
contain a large number of cells. For example, a filled square 2167
cells on a side can be stored in less than three kilobytes in
macrocell format, or about 800 bytes in compressed macrocell format.
The square's total population is over a googol, 10100; the number of
atoms in the observable universe is only about 1080.
This high level of compression is obtained by defining a tree
structure composed of increasingly large cell "tiles" with
power-of-two dimensions. Tile definitions of any size are re-used
whenever they appear multiple times in a large pattern (at the same
power-of-two offset). For example, the following is a macrocell
encoding of a complex pseudo still life arrangement of ships,
with a total population over 2500 cells:
[M2] (golly 3.0)
#R B3/S23
.OO.OO$O.O.O.O$OO...OO$$OO...OO$O.O.O.O$.OO.OO$
4 0 1 1 1
5 2 0 2 2
6 3 3 0 3
7 4 4 4 4
The first line after the #R rule line defines a quadtree tile at
the lowest level - a level-3 tile in this case, meaning a 23 square
area. At this level the pattern is encoded in a modified ASCII
format with dollar signs as line separators. The next line, #2,
defines a level-4 quadtree tile, made from one empty level-3 tile in
the northwest corner (0), and three copies of the level-3 tile that
was defined on the previous line (1). Lines 3, 4, and 5 similarly
define level 5, 6, and 7 quadtree tiles by giving the line numbers of
four tiles of the next lower size.
Many patterns are only moderately repetitive, so macrocell format
is somewhat less successful at compressing them. Certainly most
patterns are not nearly as regular as the artificial example above:
there are usually many different tiles defined at each level, not
just one. Chaotic patterns, such as ash from random soups,
usually need so many different tile definitions that they can be
stored more efficiently using rle format.
mathematician
p5
Found by Dave Buckingham, 1972.

Max
A name for the smallest known spacefiller. The name represents
the fact that the growth rate is the fastest possible. (This has not
quite been proved, however. There remains the possibility, albeit
not very likely, that a periodic agar could have an average
density greater than 1/2, and a spacefiller stretching such an agar
at the same speed as the known spacefillers would have a faster
average growth rate.)
mazing
p4
In terms of its minimum population of 12 this ties with
mold as the smallest p4 oscillator. Found by Dave Buckingham in
December 1973. For some constructions using mazings, see popover
and sixty-nine.

memory cell
A type of information storage circuit useful in many
patterns that perform complex logical operations. Most commonly a
memory cell can store a single bit of information. See for example
demultiplexer, honey bit, and boat-bit. Depending on the
application, the circuit may be a toggle circuit or a
permanent switch, or it may be possible to send one or more signals
to set the circuit to a "1" state, as can be done with a keeper
mechanism. In that case a different input signal must be used to
test the current state, usually with a destructive read reaction.
A more complicated example can be found in the Osqrtlogt pattern,
which destructively reads a growing 2-dimensional array of minimal
memory cells. Each memory cell may either contain a boat (below
left) or empty space (below right), with no permanent circuitry
anywhere near:

The two beehives and the block are placed by slow salvos, after
an initial 90-degree 2-glider collision that produces a target
honey farm. The beehive constellation acts as a one-time
turner for an incoming glider. If the boat is present, it acts
as a second one-time turner for that glider, sending back a "1"
signal. The "backstop" block in the northeast is destroyed cleanly
in either the "0" or the "1" case.
Merzenich's p11
p11
Found by Matthias Merzenich in December 2010.

Merzenich's p18
p18
Found by Matthias Merzenich in June 2011.

metacatacryst
A 52-cell pattern exhibiting quadratic growth. Found
by Nick Gotts, December 2000. This was for some time the smallest
known pattern (in terms of initial population) with superlinear
growth. See switch-engine ping-pong for the lowest-population
superlinear growth pattern as of July 2018, along with a list of
the record-holders.
metacell
CA logic circuitry that emulates the behavior of a single
cell. The circuitry is hard-wired to emulate a particular CA rule,
but changing the rule is usually a matter of making simple
adjustments. Known examples include David Bell's original 500×500
unit Life cell, Jared Prince's Deep Cell, Brice Due's
OTCA metapixel, and Adam P. Goucher's megacell.
metamorphosis II
An oscillator built by Robert Wainwright in December
1994 based on the following p30 glider-to-LWSS converter using
a queen bee shuttle pair. This converter was first found by Paul
Rendell, January 1986 or earlier, but wasn't widely known about until
Paul Callahan rediscovered it in December 1994.

Mickey Mouse
p1
The following still life, named by Mark Niemiec:
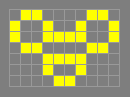
middleweight spaceship
= MWSS
mini pressure cooker
p3
Found by Robert Wainwright before June
1972. Compare pressure cooker.

M.I.P. value
The maximum population divided by the initial
population for an unstable pattern. For example, the R-pentomino
has an M.I.P. value of 63.8, since its maximum population is 319.
The term is no longer in use.
mod
The smallest number of generations it takes for an oscillator
or spaceship to reappear in its original form, possibly subject to
some rotation or reflection. The mod may be equal to the period,
but it may also be a quarter of the period (for oscillators that
rotate 90 degrees every quarter period) or half the period (for other
oscillators which rotate 180 degrees every half period, and also for
flippers).
mold
p4
Found by Achim Flammenkamp in 1988, but not widely known
until Dean Hickerson rediscovered it (and named it) in August 1989.
Compare with jam. In terms of its minimum population of 12 it
ties with mazing as the smallest p4 oscillator. But in terms of
its 6×6 bounding box it wins outright. In fact, of all oscillators
that fit in a 6×7 box it is the only one with period greater than
2.

monochromatic salvo
A slow salvo that uses gliders of only one
colour. For example, the slow salvos generated by
half-baked knightships are monochromatic, because they are
generated by a single type of reaction which can happen at any
position along a diagonal line. The smallest possible step size is
one full diagonal (1fd), which is two half diagonals (2hd), which
means that any single glider-producing reaction can only reach half
of the available glider lanes. See colour of a glider.
monogram
p4
Found by Dean Hickerson, August 1989.

Moore neighbourhood
The set of all cells that are orthogonally or
diagonally adjacent to a cell or group of cells. The Moore
neighbourhood of a cell can be thought of as the points at a
Chebyshev distance of 1 from that cell. Compare
von Neumann neighbourhood. The Conway's Life rule is based on the
Moore neighborhood, as are all the "Life-like" rules and many other
commonly investigated rule families.
Cell neighbourhoods can also be defined with a higher range. The
Moore neighbourhood of range n can be defined recursively as the
Moore neighbourhood of the Moore neighbourhood of range n-1. For
example, the Moore neighbourhood of range 2 includes all cells that
are orthogonally or diagonally adjacent to the standard Moore
neighbourhood.
moose antlers
p1

mosquito1
A breeder constructed by Nick Gotts in September 1998.
The original version had an initial population of 103, which was then
the smallest for any known pattern with superlinear growth (beating
the record previously held by Jaws). This was reduced to 97 by
Stephen Silver the following month, but was then almost immediately
superseded by mosquito2.
Mosquito1 consists of the classic puffer train plus four LWSS
and four MWSS (mostly in predecessor form, to keep the population
down). Once it gets going it produces a new block-laying
switch engine (plus a lot of junk) every 280 generations. It is
therefore an MMS breeder, albeit a messy one.
mosquito2
A breeder constructed by Nick Gotts in October 1998. Its
initial population of 85 was for a couple of hours the smallest for
any known pattern with superlinear growth, but was then beaten by
mosquito3.
Mosquito2 is very like mosquito1, but uses two fewer MWSS and
one more LWSS.
mosquito3
A breeder constructed by Nick Gotts in October 1998. Its
initial population of 75 was at the time the smallest for any known
pattern with superlinear growth, but was beaten a few days later by
mosquito4.
Mosquito3 has one less LWSS than mosquito2. It is somewhat
different from the earlier mosquitoes in that the switch engines it
makes are glider-producing rather than block-laying.
mosquito4
A slightly improved version of mosquito3 which Stephen
Silver produced in October 1998 making use of another discovery of
Nick Gotts (September 1997): an 8-cell pattern that evolves into a
LWSS plus some junk. Mosquito4 is a breeder with an initial
population of 73, at the time the smallest for any known pattern with
superlinear growth, but superseded a few days later by mosquito5.
mosquito5
A slightly improved version of mosquito4 which Nick Gotts
produced in October 1998. The improvement is of a similar nature to
the improvement of mosquito4 over mosquito3. Mosquito5 is a
breeder with an initial population of 71. This was the smallest
population for any known pattern with superlinear growth until it was
superseded by teeth. See switch-engine ping-pong for the
smallest such pattern as of July 2018, along with a list of the
record-holders.
moving sawtooth
A sawtooth such that no cell is ON for more than a
finite number generations. David Bell constructed the first pattern
of this type, with a c/2 front end and a c/3 back end. The front end
is a blinker puffer. The back end ignites the blinker fuse.
The smallest currently known moving sawtooth was constructed in
April 2011 by a conwaylife.com forum user with the handle
'cloudy197'. The c/2 front end is a bi-block puffer. The 2c/5
back end ignites the bi-block fuse.
multiple roteightors
p8
An extensible oscillator family
consisting of one or more roteightor rotors, discovered by Dean
Hickerson in 1990.

multiplicity
In a reflectorless rotating oscillator, the maximum
number n of independent patterns that can orbit a single point, in a
way that reduces the period of the combined oscillator by a factor of
n.
multum in parvo
stabilizes at time 3933
A methuselah found by
Charles Corderman, but not as long-lasting as his acorn.

MW emulator
p4
Found by Robert Wainwright in June 1980. See also
emulator and filter.
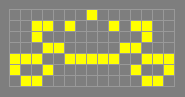
MWSS
c/2 orthogonally, p4
A middleweight spaceship, the third most
common spaceship. Found by Conway in 1970 by modifying a LWSS.
See also HWSS.
.png)
The MWSS possesses both a tail spark and a belly spark which
can easily perturb other objects as it passes by. The spaceship can
also perturb some objects in additional ways. For examples see
blinker puffer and glider turner.
Dave Buckingham found that the MWSS can be synthesized using three
gliders, and can be constructed from two gliders and another small
object in several more ways. Here is the glider synthesis:
.png)
MWSS out of the blue
The following reaction, found by Peter Rott in
November 1997, in which a LWSS passing by a p46 oscillator
creates a MWSS travelling in the opposite direction. Together with
some reactions found by Dieter Leithner, and an LWSS-turning reaction
which Rott had found in November 1993 (but which was not widely known
until Paul Callahan rediscovered it in June 1994) this can be used to
prove that there exist gliderless guns for LWSS, MWSS and HWSS
for every period that is a multiple of 46.

MW volcano
p5
Found by Dean Hickerson in April 1992.

natural
Occurring often in random patterns. There is no precise
measure of naturalness, since the most useful definition of "random"
in this context is open to debate. Nonetheless, it is clear that
objects such as blocks, blinkers, beehives and gliders are
very natural, while eater2s, darts, guns, etc., are not.
natural Heisenburp
p46
A twin bees shuttle pair arrangement found
by Brice Due in 2006. A glider passes through the reaction area of
the shuttle pair completely unaffected. However, a
Heisenburp effect causes a second glider to be created "out of the
blue", following behind the first at a 2hd offset.

negative spaceship
A type of signal travelling through a periodic
agar such as zebra stripes. The leading edge of the signal
removes the agar, and the trailing edge rebuilds the agar some time
later. The distance between the two edges is sometimes adjustable,
as shown in lightspeed bubble. The central part of the "spaceship"
may consist of dying sparks or even simple empty space.
Below is a sample period-5 negative spaceship, found by Hartmut
Holzwart in March 2007, in a small stabilized section of
zebra stripes agar:

The "spaceship" travels to the left at the speed of light, so it
will eventually reach the edge of any finite patch and destroy itself
and its supporting agar.
neighbour
Any of the eight cells adjacent to a given cell. A cell is
therefore not considered to be a neighbour of itself, although the
neighbourhood used in Life does in fact include this cell (see
cellular automaton).
new five
p3
Found by Dean Hickerson, January 1990.

new gun
p46
An old name for the period 46 glider gun show below.
This was found by Bill Gosper in 1971, and was the second basic
glider gun found (after the Gosper glider gun). It produces a
period 46 glider stream.

A number of other ways of constructing a gun from two
twin bees shuttles have since been found. See edge shooter for
one of these, and see also p46 gun.
Noah's ark
The following diagonal puffer consisting of two
switch engines. This was found by Charles Corderman in 1971. The
name comes from the variety of objects it leaves behind: blocks,
blinkers, beehives, loaves, gliders, ships, boats, long boats,
beacons and block on tables.

See also ark.
non-destructive read
A type of test reaction in memory cell
circuitry, where the information in the memory cell is unchanged and
can be read again to produce the same result. One simple type of
non-destructive read reaction is a signal sent to a
permanent switch. Memory cells with destructive read reactions
are generally simpler and more commonly used.
non-monotonic
A spaceship is said to be non-monotonic if its
leading edge falls back in some generations. The first example
(shown below) was found by Hartmut Holzwart in August 1992. This is
p4 and travels at c/4. In April 1994, Holzwart found examples of p3
spaceships with this property, and this is clearly the smallest
possible period. Another non-monotonic spaceship is the weekender.

nonomino switch engine predecessor
This is the unique nonomino (a
polyomino having 9 cells) whose evolution results in a
switch engine, and the smallest polyomino to do so.

Charles Corderman may have found this object in 1971 while
exhaustively investigating the fate of all the small polyominoes.
Records indicate that he found the switch engine while
investigating the decominoes (polyominoes having 10 cells). However,
there do not appear to be decominoes which result in a clean
switch engine. If Corderman was examining polyominoes in order of
size, then this smaller predecessor should have been found first in
any case.
non-spark
Something that looks like a spark, but isn't. An OWSS
produces one of these instead of a belly spark, and is destroyed by
it.
non-trivial
A non-trivial period-N oscillator contains at least one
cell that oscillates at the full period. In other words, it is not
made up solely of separate oscillators with smaller periods. Usually
it includes a spark or other reaction that would not occur if all
lower-period subpatterns were separated from each other, but some
exceptions are given under trivial. See also omniperiodic.
novelty generator
A pattern that appears to have an unknown fate
due to complex feedback loops, for example involving waves of
gliders shuttling between perpendicular rakes. Novelty generator
patterns fall short of counting as chaotic growth, since the rakes
continue to be predictable, and much of their ash generally remains
stable.
It has not been proven conclusively that any particular pattern is
in fact an infinite novelty generator, since it is always possible
that periodicity will spontaneously arise if the simulation is
continued far enough. In fact this happens quite regularly. But
conversely, it has not been proven that periodicity must
spontaneously arise for all such patterns. Bill Gosper, Nick Gotts
and others have done extensive experiments along these lines using
Golly.
NW31
One of the most common stable edge shooters. This
Herschel-to-glider converter suppresses the junk ordinarily left
behind by an evolving Herschel while allowing both the
first natural glider and second natural glider to escape on
transparent lanes:

The edge shooter output at the top has no additional clearance, so
its use in creating convoys is limited: it can only add gliders on
the outermost lanes of an existing glider salvo. Like the beehive
version of SW-2, either output can be used to build logical OR
gates, where multiple input signal paths are merged onto the same
output path.
The complete name for this converter is "NW31T120", where 31 is the
output glider lane number. In the above orientation, lane numbers
get bigger toward the upper right and smaller toward the lower left
(and may easily be negative).
The T120 timing measurement means that a canonical NW glider placed
on lane 31 at time T=120, at (+31, +0) relative to the input
Herschel, would in theory reach the exact same spacetime locations as
the converter's output glider does.
Most converters are not edge shooters and their output lanes are
not transparent, so they usually have catalysts that would interfere
with this theoretically equivalent glider. This is the case for the
optional third glider output created by the lower eater1 catalyst:
the upper eater1 overlaps its lane. For the alternate block
catalyst suppressing this glider output, see transparent lane.
oblique
Neither diagonal nor orthogonal. See also knightship.
obo spark
A spark of the form O.O (so called after its rle
encoding).
octagon II
p5
The first known p5 oscillator, discovered in 1971
independently by Sol Goodman and Arthur Taber. The name is due to
the latter.

octagon IV
p4
Found by Robert Wainwright, January 1979.
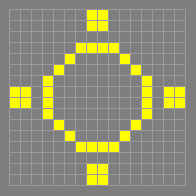
octomino
Any 8-cell polyomino. There are 369 such objects. The
word is particularly applied to the following octomino (or its
two-generation successor), which is fairly common but lacks a proper
name:

omniperiodic
A cellular automaton is said to be omniperiodic if it
has oscillators of all periods. It is not known if Life is
omniperiodic, although this seems likely. Dave Buckingham's work on
Herschel conduits in 1996 (see
My Experience with B-heptominos in Oscillators) left only a short
list of unresolved cases, all with periods of 58 or below. The list
has been progressively reduced since then. Most recently, period 43
and 53 oscillators were made possible in 2013 by Mike Playle's
Snark. As of June 2018, no oscillators are known for periods 19,
23, 38, or 41. If we insist that the oscillator must be
non-trivial, then 34 should be added to this list.
Note that if we were to allow infinite oscillators, then all
periods are certainly possible, as any period of 14 or more can be
obtained using a glider (or LWSS) stream, or an infinitely long
2c/3 wire containing signals with the desired separation.
one-sided spaceship synthesis
A glider synthesis of a spaceship
in which all gliders come from the same side of the spaceship's path.
Such syntheses are used extensively in the 17c/45 Caterpillar. For
example, here is a one-sided way to create an LWSS.

one-time
A term used for turners and splitters, specifying that
the reaction in question is not repeatable as it would be in a
reflector or fanout device. Instead, the constellation is used
up, usually in a clean reaction, but the much more common dirty
turners and splitters are also very useful in some situations.
onion rings
For each integer n>1 onion rings of order n is a stable
agar of density 1/2 obtained by tiling the plane with a certain
4n × 4n pattern. The tile for order 3 onion rings is shown below.
The reader should be able to deduce the form of tiles of other
orders.

orbit
A term proposed by Jason Summers to refer to a natural
stabilization of a puffer. For example, the switch engine has
two (known) orbits, the block-laying one and the glider-producing
one.
Orion
c/4 diagonally, p4
Found by Hartmut Holzwart, April 1993.
.png)
In May 1999, Jason Summers found the following smaller variant:
.png)
orphan
Conway's preferred term for a Garden of Eden. According to
some definitions, an orphan consists of just the minimum living and
dead cells needed to ensure that no parent is possible, whereas a GoE
is an entire infinite Life plane that contains an orphan.
Orthogonoid
256c/3476016, p3476016
A self-constructing
spaceship analogous to the Demonoids, with a slow orthogonal
direction of travel. The first example was completed by Dave Greene
on 29 June 2017, with a top speed of 16c/217251 (this is just
256c/3476016 in lowest terms).
The construction recipe is a stream of MWSSes, with the recovery
time limited to 90 ticks by the Lx200 dependent conduit that
follows the initial syringe converter. The design is
hashlife-friendly, meaning that the spaceship can be trivially
adjusted so that spatial and temporal offsets are exact powers of
two; period 4194304 and period 8388608 versions have been
constructed, with speeds of c/16384 and c/32768 respectively.
The MWSSes are converted to Herschels, which produce a standard
single-channel glider stream that runs the Orthogonoid's single
construction arm. After the child circuitry is complete, a
previously constructed Snark in the parent is removed from the
construction arm lane, converting it to a "destruction arm" that
shoots down the previous constructor/reflector in the series.
oscillator
Any pattern that is a predecessor of itself. The term
is usually restricted to non-stable finite patterns; period 1
oscillators are stable and are usually just called still lifes.
The blinker is the smallest non-stable oscillator, having period 2.
There are oscillators of almost all higher periods (see
omniperiodic). In general cellular automaton theory the term
"oscillator" usually covers spaceships as well, but this usage is
not normal in Life.
Oscillators consisting of separate objects which do not react in
any phase are usually ignored. For example, a separated blinker
and pulsar makes a period 6 oscillator, but is considered
trivial.
An oscillator can be divided into a rotor and a stator, and the
stator can be further subdivided into bushing and casing. Some
oscillators have no casing cells, and a few 100%-volatility
oscillators also have no bushing cells.
An oscillator can be constructed from any gun as long as eaters
can be added to consume its output. If it is a true gun then the
period of the oscillator will be the same as the gun - unless the
eating mechanism multiplies the period, as in the case of gliders
caught by a boat-bit.
With the discovery of reflectors, relays provide an easy way to
create oscillators of all large periods. For example, eight gliders
travelling in a loop created by four Snarks can create any period
above 42, with a population never exceeding 356 live cells.
For the very lowest periods, whole families of extensible
oscillators are known. Examples of this are barberpole, cross,
pentoad, p6 shuttle, snacker, and multiple roteightors. Any
of the shuttles are oscillators by definition, for example the
queen bee shuttle. Many of these are also extensible. Other
oscillators such as figure-8 and tumbler have unique mechanisms
that are not part of an extended family.
Some oscillators are useful because of the perturbations they can
cause to other objects. This is especially true if they provide a
spark on their boundary. Some oscillators are explicitly found by
search programs in order to produce these sparks, such as
pipsquirters.
Some higher period oscillators have been found while running random
soups. This is especially true if the soup is run on a cylindrical
or torus universe. Sometimes the found objects can be moved to the
normal universe and supported there by added catalysts.
Achim's p144 is an example.
Osqrtlogt
p1 circuitry
A pattern constructed by Adam P. Goucher in
2010, which uses an unbounded triangular region as memory for a
binary counter. Empty space is read as a zero, and a boat as a one,
as shown in the example pattern in memory cell. The pattern's
diametric growth rate is O(sqrt(log(t))), which is the slowest
possible for any Life pattern, or indeed any 2D Euclidean cellular
automaton. The population returns infinitely often to its initial
minimum value (during carry operations from 11111...1 to 100000...0,
so it can be considered to be an unusual form of sawtooth.
OTCA metapixel
p46 circuitry
A 2048 × 2048 period 35328 metacell
constructed by Brice Due in 2006. It contains a large "pixel" area
that contains a large population of LWSSes when the metacell state
is ON, but is empty when it is OFF. This allows the state of the
metacell to be visible at high zoom levels, unlike previous
unit cells where the state was signaled by the presence or absence
of a single glider in a specific location.
out of the blue
See natural Heisenburp. Other similar mechanisms,
particularly the method of LWSS creation used in the pixel part of
the OTCA metapixel, may also be referred to as "out of the blue"
reactions.
overclocking
A term used when a circuit can accept a signal at a
specific period which it cannot accept at a higher period. A
syringe is a simple example.
Some staged recovery circuits also permit overclocking, and can
function successfully at a rate faster than their recovery time. A
Silver reflector has a recovery time of 497 ticks, but can be
overclocked to reflect a period 250 glider stream, or any nearby
period above 248, simply by removing a beehive after the first glider
enters the reflector. However, a continuous stream of gliders is
then required to maintain the circuit, with timing within a tightly
bounded range.
over-unity reaction
An important concept in gun and
macro-spaceship construction. To be a good candidate for building
one of these types of patterns with a new period or speed, a
stationary reaction (for a gun) or a moving reaction (for a
macro-spaceship) must be able to produce some number of output
signals, strictly greater than the number of input signals required
to maintain the reaction. The extra signal becomes a gun's output
stream, or may be used in a variety of ways to construct the
supporting track for a macro-spaceship. By implication,
"over-unity" refers to the ratio of output signals to input signals.
If all signal outputs must be used up to sustain a stationary
reaction, a high-period oscillator may still be possible. See
emu for example.
overweight spaceship
= OWSS
OWSS
A would-be spaceship similar to LWSS, MWSS and HWSS but
longer. On its own an OWSS is unstable, but it can be escorted by
true spaceships to form a flotilla.
Ox
A 1976 novel by Piers Anthony which involves Life.
p11 bumper
p11
A periodic colour-preserving glider reflector
with a minimum repeat time of 44 ticks. Unlike the p5 through p8
cases where Noam Elkies' domino-spark based reflectors are
available, no small period-22 colour-changing reflector is known.
A stable Snark reflector can be substituted for any bumper.
This changes the timing of the output glider, which can be useful for
rephasing periodic glider streams.

In practice this reflector is not useful with input streams below
period 121, because lower-period bumpers can be used to reflect all
smaller multiples of 11 for which the bumper reaction can be made to
work.
p130 shuttle
A shuttle found in March 2004 by David Eppstein, which
originally needed several period 5 oscillators for support. David
Bell found a reaction between two of the shuttles to produce a p130
glider gun. On 18 November 2017 Tanner Jacobi found that the
stable sidesnagger can be used to support the shuttle instead,
and this is shown here.

p144 gun
A glider gun with true period 144. The first one was
found by Bill Gosper in July 1994. For a full description and
pattern see factory.
p14 gun
A glider gun which emits a period 14 glider stream. This is
the smallest possible period for any stream, so such a gun is of
great interest. There is no known true-period p14 glider gun, and
finding a small direct example is well beyond current search
algorithms' abilities. However, pseudo-period p14 guns have been
created by injecting gliders into a higher period glider stream.
The first pseudo p14 gun was built by Dieter Leithner in 1995.
Smaller pseudo p14 guns have since been constructed, but they are
still much too large to show here. The essential mechanism used by
them is demonstrated in GIG.
p184 gun
A true period 184 double-barrelled glider gun found by
Dave Buckingham in July 1996. The engine in this gun is a
Herschel descendant. Unlike previous glider guns, the reaction
flips on a diagonal so that both gliders travel in the same
direction.

p1 megacell
p1 circuitry
A metacell constructed by Adam P.
Goucher in 2008, capable of being programmed to emulate any Moore
neighborhood rule, including isotropic and anisotropic non-totalistic
rules. It fits in a 32768 by 32768 bounding box, with the resulting
metacell grid at 45 degrees to the underlying Life grid. Like the
OTCA metapixel, it includes a large "pixel" area so that the state
of the megacell can easily be seen even at extremely small-scale zoom
levels.
p1 telegraph
p1 circuitry
A variant of Jason Summers' telegraph
pattern, constructed in 2010 by Adam P. Goucher using only stable
circuitry. A single incoming glider produces the entire ten-part
composite lightspeed signal that restores the beehive-chain
lightspeed wire to its original position. The signal is detected
at the other end of the telegraph and converted back into a single
output signal. This simplification came at the cost of a much slower
transmission speed, one bit per 91080 ticks. In this mechanism,
sending the entire ten-part signal constitutes a '1' bit, and not
sending the signal means '0'. See also high-bandwidth telegraph.
p22 gun
A true period 22 glider gun constructed by David Eppstein
in August 2000, using two interacting copies of a p22 oscillator
found earlier the same day by Jason Summers.

p246 gun
A true period glider gun with period 246, discovered by
Dave Buckingham in June 1996. The 180-degree mod-123 symmetry of its
bookend-based engine makes it trivial to modify it into a
double-barrelled gun. Its single-barreled form is shown below.

p24 gun
A glider gun with true period 24. The first one was
found by Noam Elkies in June 1997. It uses three p4 oscillators to
hassle a pair of traffic lights. One of the oscillators was very
large and custom-made. Shown below is a much smaller version built
by Jason Summers and Karel Suhajda in December 2002, using the same
mechanism but with a smaller oscillator:

p256 gun
A true period 256 four-barrelled glider gun found by
Dave Buckingham in September 1995. It uses four R64 conduits to
make the second smallest known Herschel loop (after the
Simkin glider gun). The p256 gun was an early "teaser" from Dave
Buckingham before he released his full Herschel technology.

Either eaters or snakes can be added as shown above, to suppress
three of the glider streams so that only one stream escapes. This
gun's p256 glider stream is well-suited for repeated reactions with
receding Corderships, or for "Hashlife-friendly" signal
circuitry.
p29 pentadecathlon hassler
A hassler where two copies of a period
29 oscillator (which is itself a pre-pulsar hassler) change the
period of a pentadecathlon.

p30 gun
A glider gun with true period 30. The first one, found
by Bill Gosper in November 1970 (see Gosper glider gun), was also
the first gun found of any period. All known p30 glider guns are
made from two or more interacting queen bee shuttles. Paul Callahan
found 30 different ways that three queen bee shuttles can react to
form a period 30 glider gun. One of the most interesting of these is
shown below in which the gliders emerge in an unexpected direction.

p36 gun
A glider gun with true period 36. The first one was found
by Jason Summers in 2004. Shown below is a smaller version using
improvements by Adam P. Goucher and Scot Ellison:

p3 bumper
A variant of Tanner Jacobi's bumper found by Arie Paap in
April 2018. Two forms of the period 3 oscillator catalyst are
shown below.
.png)
For bounding box optimization purposes, it's also possible to
replace the eater1 in a p3, p6 or p9 bumper with another period 3
oscillator, saving one row along the south edge at the cost of a
higher population.
.png)
The repeat time for all these variants is 36 ticks, as shown.
p44 gun
A glider gun with a true period of 44. The first one was
found by Dave Buckingham in April 1992. It uses two interacting
copies of an oscillator which he also found. In 1996 he found a
gun which only used one copy of the oscillator. Paul Callahan
improved it in 1997, resulting in the gun shown below:
p44 MWSS gun
A gun discovered by Dieter Leithner in April 1997, in a
somewhat larger form. This was the smallest known gliderless gun and
smallest known MWSS gun until the construction in 2017 of the gun
shown under gliderless, based on Tanner's p46.
The p44 MWSS gun is based on a p44 oscillator discovered by Dave
Buckingham in early 1992, shown here in an improved form found in
January 2005 by Jason Summers using a new p4 sparker by Nicolay
Beluchenko. A glider shape appears in this gun for three consecutive
generations, but always as part of a larger cluster, so even a
purist would regard this gun as gliderless.

p45 gun
A true-period glider gun discovered by Matthias Merzenich
in April 2010. By most measures this is the smallest known
odd-period gun of any type, either true-period or pseudo-period:

p4 bumper
p4
A periodic colour-preserving glider reflector
with a minimum repeat time of 36. Unlike the p5 through p8 cases
where Noam Elkies' domino spark-based reflectors are available, no
small period-4 colour-changing reflector is known. A stable
Snark reflector can be substituted for any bumper. This changes
the timing of the output glider, which can be useful for rephasing
periodic glider streams.
p4 reflector
The following glider reflector, discovered by Karel
Suhajda in October 2012. Its minimum repeat time is 52 ticks.
Unlike the various bouncers discovered many years earlier, it is a
colour-preserving reflector, so it was made obsolete the following
year by the discovery of the much smaller stable Snark, which uses
the same initial bait reaction and so produces an output glider
with the same timing. For a smaller periodic colour-preserving
glider reflector with a different output timing, see p4 bumper.

p5 reflector
Traditional name for p5 bouncer before 2016, but with
the discovery of the p5 bumper this has become an ambiguous
reference.
p60 gun
A glider gun with a true period of 60. The first one was
found by Bill Gosper in 1970 and is shown below.

There are several other ways to create a p60 gun from two p30 guns
using period-doubling reactions similar to the one shown here.
p690 gun
A true period 690 glider gun found by Noam Elkies in
July 1996. It is composed of a p30 queen bee shuttle pair and a
p46 twin bees shuttle whose sparks occasionally react with each
other. This is a very compact gun for such a high period and is used
in many patterns requiring sparse glider streams.

p6 reflector
Traditional name for p6 bouncer before 2016, but with
the discovery of the p6 bumper this has become an ambiguous
reference.
p6 shuttle
p6
The following oscillator found by Nicolay Beluchenko
in February 2004.
.png)
This is extensible in more than one way:
.png)
p72 quasi-shuttle
p72
The following oscillator, found by Jason
Summers in August 2005. Although this looks at first sight like a
shuttle, it isn't really.

p7 pipsquirter
A pipsquirter oscillator found by Noam Elkies in
August 1999, used in various hasslers and the colour-changing
p7 reflector.
.png)
A larger period-7 pipsquirter is used in cases where space is
limited where the reflector should extend southward for as short a
distance as possible:
.png)
p7 reflector
Traditional name for p7 bouncer before 2016, but with
the discovery of the p7 bumper this has become an ambiguous
reference.
p8 reflector
Traditional name for p8 bouncer before 2016, but with
the discovery of the p8 bumper this has become an ambiguous
reference.
p90 gun
A glider gun with true period 90. The one below by Dean
Hickerson uses the output of two p30 guns in a period-multiplying
reaction:

p92 gun
A glider gun with a true period of 92. The first one was
found by Bill Gosper in 1971 using a period doubling reaction using
two p46 guns. Many different p92 guns are known that use multiple
twin bees shuttles. A period 92 gun can also be made by adding a
semi-cenark to any period 46 glider gun.
On 18 November 2017, Martin Grant found a new gun using one twin
bees shuttle and one Tanner's p46 oscillator, making it the
smallest known p92 gun.

Parallel HBK
(6,3)c/245912, p245912
A much smaller successor to the
half-baked knightship, constructed by Chris Cain in September 2014.
Several slow-salvo recipes are needed to support the multi-glider
salvo seeds at the upstream end of the spaceship. "Parallel" means
that these recipes are sent in parallel instead of one after the
other, in series, as in the original HBK.
Parallel HBK gun
An armless constructor pattern that is programmed
to build Parallel HBK oblique spaceships every 125906944 ticks.
This gun was created by Chris Cain on 3 January 2015.
parasite
A self-sustaining reaction attached to the output of a rake
or puffer, that damages or modifies the standard output. Compare
tagalong. In 2009, while experimenting with novelty generator
patterns in Golly, Mitchell Riley discovered parasites on glider
streams from p20 and p8 backward rakes. In some cases, parasites can
even "reproduce", as in the pattern below, though the number of
copies is limited since they will eventually use up their host glider
stream:

parent
A pattern is said to be a parent of the pattern it gives rise
to after one generation. Some patterns have infinitely many parents,
but others have none at all (see Garden of Eden). Typically
parents are considered trivial if they contain groups of cells that
can be removed without changing the result, such as isolated faraway
cells.
parent cells
The three cells that cause a new cell to be born.
parity
Even or odd, particularly as applied to the phase of an
oscillator or spaceship. For example, in slow salvo constructions,
the intermediate targets are frequently period 2, most often
because they contain blinkers or traffic lights. A glider
striking a P2 constellation will generally produce a different result
depending on its parity. Period-4 intermediate targets are rare (or
not used), so it doesn't matter for example whether an odd-parity
glider in a slow salvo is phase 1 or phase 3. Only the even/odd
parity is important.
partial result
An intermediate object found by a search program
which might be a substantial part of a complete spaceship or
oscillator, but which isn't complete.
Running a partial result works for a few generations until the
speed of light corruption from any unfinished edge destroys the
whole object. But a partial result can still be used to see whether
the object (if ever finished) would provide a desired spark or
perturbation. If no partial results are found then it is likely
that no such object exists under the constraints of the search.
Very large partial results can indicate that there is a good chance
that the object being searched for might actually exist (but this is
no guarantee). Rerunning the search using the partial result as a
base and relaxing some constraints, widening or adjusting the search
area, or splitting the object into multiple arms might result in
finding a complete working object.
As an example, here is a large partial result for a period 6
knightship found by Josh Ball in April 2017. The first 22 columns
were rediscovered in 2018 as part of the successful search for
Sir Robin. See also almost knightship for an earlier small
example by Eugene Langvagen.

pedestle
p5
An oscillator found by Dave Buckingham in 1973.

penny lane
p4
Found by Dave Buckingham, 1972.

pentadecathlon
p15
Found in 1970 by Conway while tracking the
history of short rows of cells, 10 cells giving this object, which is
the most natural oscillator of period greater than 3. In fact it
is the fifth most common oscillator overall, appearing in random
soups slightly more frequently than the clock, but much less
frequently than the blinker, toad, beacon or pulsar. The
pentadecathlon can be constructed using just three gliders, as shown
in glider synthesis.

The pentadecathlon is the only known oscillator that has two
phases that are different polyominoes. It produces accessible
V sparks and domino sparks, which give it a great capacity for
doing perturbations, especially for period 30 based technology.
See relay for example.
pentant
p5
Found by Dave Buckingham, July 1976.

pentoad
p5
Found by Bill Gosper, June 1977. This is extensible:
if an eater is moved back four spaces then another Z-hexomino can
be inserted. (This extensibility was discovered by Scott Kim.)

pentomino
Any 5-cell polyomino. There are 12 such patterns, and
Conway assigned them all letters in the range O to Z, loosely based
on their shapes. Only in the case of the R-pentomino has Conway's
label remained in common use, but all of them can nonetheless be
found in this lexicon.
periodic
For circuit mechanisms, "periodic" is the opposite of p1
or stable. Periodic circuits necessarily contain oscillators,
and therefore they can generally only accept input signals that are
synchronized to the combined period of those oscillators (but see
universal regulator).
For signal streams, "periodic" means that signals will only be
present in the stream at one out of every n ticks, where n is the
period of the stream. In a periodic intermittent stream there
may be gaps, so that signals do not always appear at every nth tick.
However, if a signal does appear, its distance measured in ticks from
previous and future signals will always be an exact multiple of n.
period multiplier
A term commonly used for a pulse divider, because
dividing the number of signals in a regular stream by N necessarily
multiplies the period by N. The term "period multiplier" can be
somewhat misleading in this context, because most such circuits can
accept input streams that are not strictly periodic.
Reactions have also been found to period double or period triple
the output of some rakes to create high-period rakes in a
relatively small space (i.e., an exponential increase in period for a
linear increase in size).
For Herschel signals and glider guns, a number of small period
doubler, tripler, and quadrupler mechanisms are known. For example,
the following conduit produces one output glider after accepting
four input B-heptominoes, or four Herschels if a conduit such as
F117 is prepended that includes the same BFx59H converter.

See semi-Snark and tremi-Snark for additional examples using
glider streams. As of June 2018 no stable period-multiplying
elementary conduits are known for a multiplication factor of five
or higher, though it is easy to construct composite ones.
permanent switch
A signal-carrying circuit that can be modified
so that it cleanly absorbs any future signals instead of allowing
them to pass. Optionally there may be a separate mechanism to
restore the circuit to its original function.
In the following example, a glider from the northeast (shown) will
perform a simple block pull that switches off an F166 conduit, so
that any future Herschel inputs will be cleanly absorbed. A glider
from the southwest (also shown) can restore the block to its original
position.

perturb
To change the fate of an object by reacting it with other
objects. Typically, the other objects are sparks from spaceships
or oscillators, or are eaters or impacting spaceships.
Perturbations are typically done to turn a dirty reaction into a
clean one, or to change the products of a reaction. In many
desirable cases the perturbing objects are not destroyed by the
reaction, or else are easily replenished.
PF35W
One of the three elementary conduits used in the composite
Fx176 Herschel conduit. It converts an input pi-heptomino into
an output wing in 35 ticks. In November 2017, Aidan F. Pierce
discovered the compact PF35W variant below, which improved the repeat
time of the Fx176 to 73 ticks and allowed gliders from following
dependent conduits to escape freely:
.png)
Several variants of the key catalyst are known, including welded
additions for the Fx176 that absorb the following Herschel's first
natural glider, since a standard fishhook eater doesn't quite fit.
The following is a complete Fx176 conduit incorporating the new
PF45W:
.png)
phase
A representative generation of a periodic object such as an
oscillator or spaceship. The number of phases is equal to the
period of the object. The phases of an object usually repeat in
the same cyclic sequence forever, although some perturbations can
cause a phase change.
phase change
A perturbation of a periodic object that causes the
object to skip forward or backward by one or more phases. If the
perturbation is repeated indefinitely, this can effectively change
the period of the object. An example of this, found by Dean
Hickerson in November 1998, is shown below. In this example, the
period of the oscillator would be 7 if the mold were removed, but
the period is increased to 8 because of the repeated phase changes
caused by the mold's spark.
.png)
The following pattern demonstrates a p4 c/2 spaceship found by
Jason Summers, in which the phase is changed as it deletes a
forward glider. This phase change allows the spaceship to be used
to delete a glider wave produced by a rake whose period is 2 (mod
4).
.png)
Phase changing reactions have enabled the construction of
spaceships having periods that were otherwise unknown, and also allow
the construction of period-doubling and period-tripling convoys to
easily produce very high period rakes.
See also blinker puffer.
phi
The following common spark. The name comes from the shape in
the generation after the one shown here.

One oscillator which produces this spark is Tanner's p46. The
pentadecathlon produces a slightly corrupted version of this spark.
phoenix
Any pattern all of whose cells die in every generation, but
which never dies as a whole. A spaceship cannot be a phoenix, and
in fact every finite phoenix eventually evolves into an oscillator.
The following 12-cell oscillator (found by the MIT group in December
1971) is the smallest known phoenix, and is sometimes called simply
"the phoenix".
.png)
This is extensible and is just the first of a family of phoenixes
made by joining components together to form a loop. Here is
another member of this family.
.png)
Every known phoenix oscillator has period 2. In January 2000,
Stephen Silver showed that a period 3 oscillator cannot be a phoenix.
The situation for higher periods is unknown.
An easy synthesis of the phoenix is possible using four blocks as
seeds. A puffer creating a growing row of phoenixes has the
unusual property that the percentage of live cells that stay alive
for more than one generation approaches zero. See lone dot agar
for an example of an infinite phoenix.
Pianola breeder
A series of patterns by Paul Tooke in 2010, based on
a simplification and extension of the Gemini spaceship's
construction mechanism. Tooke produced a number of
slow-salvo-constructed patterns with superlinear growth, including
a series of breeder patterns of previously unknown types. For some
patterns, the Gemini's two construction arms were moved to a
permanent stationary platform, using fourteen glider-loop channels
instead of twelve.
Some of these breeder patterns remain difficult to classify
unambiguously. For example, one pattern was designed to be an MSS
breeder - a modified Gemini spaceship puffing slide guns which
build lines of blocks. However, the slide guns produce both moving
and stationary objects at a linear rate, because streams of gliders
are needed to reach out to the construction zone to do the push
reaction and build more blocks. The pattern could therefore be
classified as a hybrid MSM/MSS breeder. Other breeder patterns
utilizing slide guns and universal constructor technology are
likely to cause similar classification ambiguities.
pi calculator
p1 circuitry
A device constructed by Adam P. Goucher
in February 2010, which calculates the decimal digits of pi (the
transcendental number, not the Life pattern!) and displays them in
the Life universe as 8×10 dot matrix characters formed by
arrangements of blocks along a diagonal stripe at the top. A push
reaction moves a ten-block diagonal cursor to the next position as
part of the "printing" operation for each new digit.
The actual calculation is done in binary, using a streaming spigot
algorithm based on linear fractional transformations. The pi
calculator is made up of a 188-state computer connected to a printing
device via period-8 regulators and a binary-to-decimal conversion
mechanism. The complete pattern can be found in Golly's Very Large
Patterns online archive, along with the very similar 177-state phi
calculator which uses a simpler algorithm to calculate and print the
Golden Ratio.
pi climber
The reaction that defines rate of travel of the
Caterpillar spaceship. A pi climber consists of a pi-heptomino
"climbing" a chain of blinkers, moving 17 cells every 45 ticks, and
leaving behind an identical chain of blinkers, shifted downward by 6
cells. A single pi climber does not produce any gliders or other
output, but two or more of them travelling on nearby blinker chains
can be arranged to emit gliders every 45 ticks. Compare
Herschel-pair climber.

pi-heptomino
stabilizes at time 173
A common pattern. The name is
also applied to later generations of this object. In a pi ship,
for example, the pi-heptomino itself never arises.

pinwheel
p4
Found by Simon Norton, April 1970. Compare clock II.

pi orbital
p168
Found by Noam Elkies, August 1995. In this
oscillator, a pi-heptomino is turned ninety degrees every 42
generations. A second pi can be inserted to reduce the period to 84.

pi portraitor
p32
Found by Robert Wainwright in 1984 or 1985.
Compare with gourmet and popover.

pi ship
A growing spaceship in which the back part consists of a
pi-heptomino travelling at a speed of 3c/10. The first example was
constructed by David Bell. All known pi ships are too large to show
here, but the following diagram shows how the pi fuse works.

piston
p2
Found in 1971.

pi wave
A line of pi-heptominoes stabilizing one another. For
example, an infinite line of pi-heptominoes arranged as shown below
produces a pi wave that moves at a speed of 3c/10 with period 30, and
leaves no debris.

polyomino
A finite collection of orthogonally connected cells. The
mathematical study of polyominoes was initiated by Solomon Golomb in
1953. Conway's early investigations of Life and other cellular
automata involved tracking the histories of small polyominoes, this
being a reasonable way to ascertain the typical behaviour of
different cellular automata when the patterns had to be evolved by
hand rather than by computer. Polyominoes have no special
significance in Life, but their extensive study during the early
years lead to a number of important discoveries and has influenced
the terminology of Life. (Note on spelling: As with "dominoes" the
plural may also be spelt without an e. In this lexicon I have
followed Golomb in using the longer form.)
It is possible for a polyomino to be an oscillator. In fact
there are infinitely many examples of such polyominoes, namely the
cross and its larger analogues. The only other known examples are
the block, the blinker, the toad, the star and (in two
different phases) the pentadecathlon.
A polyomino can also be a spaceship, as the LWSS, MWSS and
HWSS show.
polyplet
A finite collection of orthogonally or diagonally connected
cells. This king-wise connectivity is a more natural concept in Life
than the orthogonal connectivity of the polyomino.
pond
p1

population
The number of ON cells.
P-pentomino
Conway's name for the following pentomino, a common
spark.

PPS
c/5 orthogonally, p30
A pre-pulsar spaceship. Any of three
different p30 c/5 orthogonal spaceships in which a pre-pulsar is
pushed by a pair of spiders. The back sparks of the spaceship can
be used to perturb gliders in many different ways, allowing the easy
construction of c/5 puffers. The first PPS was found by David Bell
in May 1998 based on a p15 pre-pulsar spaceship found by Noam Elkies
in December 1997. See also SPPS and APPS.
The pattern below shows the basic mechanism of a PPS. The two
isolated sparks at the left and right sides are the edge sparks
from the two supporting spiders.
pre-block
The following common parent of the block. Another such
pattern is the grin.

predecessor
Any pattern that evolves into a given pattern after one
or more generations.
pre-pre-block
A common predecessor to the pre-block (and thus the
block):
.png)
This is easily created by a two-glider collision. Hitting the
pre-pre-block with a glider can create a MWSS. Both of these
reactions are shown below:
.png)
pre-pulsar
A common predecessor of the pulsar, such as that shown
below. This duplicates itself in 15 generations. (It fails,
however, to be a true replicator because of the way the two copies
then interact.)

A pair of tubs can be placed to eat half the pre-pulsar as it
replicates; this gives the p30 oscillator Eureka where the
pre-pulsar's replication becomes a movement back and forth. See
twirling T-tetsons II for a variation on this idea. By other means
the replication of the pre-pulsar can be made to occur in just 14
generations as half of it is eaten; this allows the construction of
p28 and p29 oscillators. The pre-pulsar was also a vital component
of the first known p26 and p47 oscillators.
See also PPS.
pre-pulsar spaceship
= PPS.
primer
A pattern originally constructed by Dean Hickerson in November
1991 that emits a stream of LWSSs representing the prime numbers.
Some improvements were found by Jason Summers in October 2005.
protein
p3
Found by Dave Buckingham, November 1972.

pseudo
Opposite of true. A gun emitting a period n stream of
spaceships (or rakes) is said to be a pseudo period n gun if its
mechanism oscillates with a period greater than n. This period will
necessarily be a multiple of n. If the base mechanism's period is
instead a fraction of n, then a period multiplier must also be
present which is considered to be part of the mechanism, and the gun
as a whole is still a true period gun. For example, a filter may
be used on a lower-period gun to produce a compound gun such as the
true p48 gun.
Pseudo period n glider guns are known to exist for all periods
greater than or equal to 14, with smaller periods being impossible.
All known p14 guns are pseudo guns requiring several signal
injections, so they are quite large. The following smaller example
is a pseudo period 123 gun, interleaving the streams from two true
period 246 guns:

The same distinction between true and pseudo also exists for
puffers.
pseudo-barberpole
p5
Found by Achim Flammenkamp in August 1994. In
terms of its minimum population of 15 this is the smallest known p5
oscillator. See also barberpole.

pseudo-random glider generator
A pseudo-random number generator in
which the bits are represented by the presence or absence of
gliders. The first pseudo-random glider generator was built by
Bill Gosper. David Bell built the first moving one in 1997, using
c/3 rakes.
pseudo-random number generator
A pseudo-random number generator
(PRNG) is an algorithm that produces a sequence of bits that looks
random (but cannot really be random, being algorithmically
determined).
In Life, the term refers to a PRNG implemented as a Life pattern,
with the bits represented by the presence or absence of objects such
as gliders or blocks. Such a PRNG usually contains gliders or
other spaceships in a loop with a feedback mechanism that causes
later spaceships to interfere with the generation of earlier
spaceships. The period can be very high, as a loop of n spaceships
has 2n possible states.
pseudo still life
A stable pattern whose live cells are either
immediately adjacent to each other, or are connected into a single
group by adjacent dead cells where birth is suppressed by
overpopulation.
The definition of strict still life rules out such stable
patterns as the bi-block. In such patterns there are dead cells
which have more than 3 neighbours in total, but fewer than 3 in any
component still life. These patterns are called pseudo still lifes,
and have been enumerated up to 32 bits, as shown in the table below.
--------------
Bits Number
--------------
8 1
9 1
10 7
11 16
12 55
13 110
14 279
15 620
16 1645
17 4067
18 10843
19 27250
20 70637
21 179011
22 462086
23 1184882
24 3068984
25 7906676
26 20463274
27 52816265
28 136655095
29 353198379
30 914075620
31 2364815358
32 6123084116
--------------
Attribution of these counts is given in strict still life; see
also https://oeis.org/A056613. The unique 32-bit triple pseudo
still life is included in the last count in the table. As the number
of bits increases, the pseudo still life count goes up exponentially
by approximately O(2.56n). By comparison, the rate for
strict still lifes is about O(2.46n) while for quasi still lifes
it's around O(3.04n).
If a stable pattern's live cells plus its overpopulated dead cells
do not form a single mutually adjacent group, the pattern is usually
referred to as a constellation. It is also a still life in the
general sense, but is neither "pseudo" nor "strict".
puffer
An object that moves like a spaceship, except that it leaves
debris behind. The first known puffers were found by Bill Gosper and
travelled at c/2 orthogonally (see diagram below for the very first
one, found in 1971).
Not long afterwards c/12 diagonal puffers were found (see
switch engine). Discounting wickstretchers, which are not
puffers in the conventional sense, no new velocity was obtained after
this until David Bell found the first c/3 orthogonal puffer in April
1996. Other new puffer speeds followed over the next several years.
Many spaceships that travel orthogonally at a speed less than c/2
have useful side or back sparks. These can be used to perturb
standard spaceships that approach from behind. A common technique
for creating puffers for a new speed uses a convoy of the new
spaceships to create debris from an approaching standard spaceship
such that a new standard spaceship is recreated on the same path as
the original one. This forms a closed loop, resulting in a
high-period puffer for the new speed.
As of June 2018, puffers have been found matching every known
velocity of elementary spaceship, except for c/6 and c/7 diagonal
and (2,1)c/6. It is also generally easy to create puffers based on
macro-spaceships, simply by removing some part of the trailing
cleanup mechanism.
puffer engine
A pattern which can be used as the main component of a
puffer. The pattern may itself be a puffer (e.g. the classic
puffer train), it may be a spaceship (e.g. the Schick engine), or
it may even be unstable (e.g. the switch engine).
pufferfish
c/2, p12
A puffer discovered by Richard Schank in
November 2014, from a symmetric soup search using an early version of
apgsearch. It consists of a pair of B-heptominoes stabilised by
a backend that leaves only pairs of blocks behind. It is simple
enough to be easily synthesized with gliders.

See soup for a random initial pattern, generated by apgsearch and
recorded in Catagolue, that produces a pufferfish.
pufferfish spaceship
c/2, p36
Generally, any spaceship
constructed using pufferfish. May refer specifically to the
extensible c/2 spaceship constructed by Ivan Fomichev in December
2014, the first such spaceship to contain no period-2 or period-4
parts. (The first two or three rows might be considered to be period
2 or 4, but they are directly dependent on following rows for
support.).
The pattern consists of two adjacent pufferfish puffers, plus
four copies of a nontrivial period 36 c/2 fuse for pufferfish
exhaust, discovered using a randomized soup search.

puffer train
The full name for a puffer, coined by Conway before
any examples were known. The term was also applied specifically to
the classic puffer train found by Bill Gosper and shown below. This
is very dirty, and the tail does not stabilize until generation
5533. It consists of a B-heptomino (shown here one generation
before the standard form) escorted by two LWSS. (This was the
second known puffer. The first is shown under puffer.)
.png)
In April 2006, Jason Summers found a way to make the classic puffer
train into a p20 spaceship by adding a glider at the back:
.png)
puff suppressor
An attachment at the back of a line puffer that
suppresses all or some of its puffing action. The example below (by
Hartmut Holzwart) has a 3-cell puff suppressor at the back which
suppresses the entire puff, making a p2 spaceship. If you delete
this puff suppressor then you get a p60 double beehive puffer.
Puff suppressors were first recognised by Alan Hensel in April 1994.

pulsar
p3
Despite its size, this is the fourth most common
oscillator (and by far the most common of period greater than 2)
and was found very early on by Conway. See also pre-pulsar,
pulsar quadrant, and quasar.

pulsar CP 48-56-72
= pulsar (The numbers refer to the populations
of the three phases.)
Pulsar Pixel Display
p30 circuitry
A large-scale raster line
display device constructed by Mark Walsh in August 2010, where
pulsars form the individual pixels in an otherwise empty grid. The
published sample pattern displays and erases eight 7×5-pixel
characters on each of two lines of text.
pulse divider
A mechanism that lets every n-th object that reaches it
pass through, and deletes all the rest, where n > 1 and the objects
are typically gliders, spaceships or Herschels. A common
synonym is period multiplier. For n=2, the simplest known stable
pulse dividers are the semi-Snarks.
The following diagram shows a p5 glider pulse divider by Dieter
Leithner (February 1998). The first glider moves the centre block
and is reflected at 90 degrees. The next glider to come along will
not be reflected, but will move the block back to its original
position. The relatively small size and low period of this example
made it useful for constructing compact glider guns of certain
periods, but it became largely obsolete with the discovery of the
stable CC semi-Snark, which uses the same basic mechanism.
Period 7, 22, 36 and 46 versions of this pulse divider are also
known.

pulshuttle V
p30
Found by Robert Wainwright, May 1985. Compare
Eureka.

pure glider generator
A pattern that evolves into one or more
gliders, and nothing else. There was some interest in these early
on, but they are no longer considered important. Here's a neat
example:
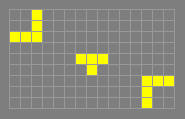
pushalong
Any tagalong at the front of a spaceship. The following
is an example found by David Bell in 1992, attached to the front of a
MWSS.

pyrotechnecium
p8
Found by Dave Buckingham in 1972.

pyrotechneczum
A common mistaken spelling of pyrotechnecium, caused
by a copying error in the early 1990s.
quad
p2
Found by Robert Kraus, April 1971. Of all oscillators
that fit in a 6×6 box this is the only flipper.

QuadLife
A form of colourised Life in which there are four types of
ON cell. A newly-born cell takes the type of the majority of its
three parent cells, or the remaining type if its parent cells are
all of different types. In areas where there are only two types of
ON cell QuadLife reduces to Immigration.
quad pseudo
A still life that can be broken down into four stable
pieces but not into two or three. This term may refer to the
following 34-bit pattern, found by Gabriel Nivasch in July 2001, or
any similar pattern with the same property.

As a consequence of the Four-Colour Theorem, there can be no
analogous objects requiring decomposition into five or more pieces.
By convention, patterns like this and the triple pseudo are
considered to be pseudo still lifes, not strict still lifes. As
of June 2018, it has been shown that no quad pseudo patterns exist
with 32 or fewer bits, but a 33-bit pattern with this property may
theoretically still be found.
quadratic filter
A toolkit developed by Dean Hickerson and Gabriel
Nivasch in 2006, enabling the construction of patterns with
asymptotic population growth matching an infinite number of different
sublinear functions - namely, O(t(1/2n)) for any chosen n. See
also exponential filter, recursive filter.
quadratic growth
The fastest possible asymptotic rate of population
growth for any Life pattern - O(t2) in big-O notation, where t is
the number of ticks. The first quadratic-growth pattern found was
Bill Gosper's 1971 breeder. Many other types of breeders and
spacefillers have been constructed since.
In April 2011, Stephen Silver gave an example of a one-cell-thick
pattern over a million cells long that exhibited quadratic growth.
In October 2015, Chris Cain constructed a one-cell-thick pattern with
a reduced bounding box of 2596×1, improving on a series of previous
longer results. The smallest known quadratic growth pattern by
initial population is the 23-cell switch-engine ping-pong by
Michael Simkin.
There are an infinite number of possible growth rates between
linear and quadratic growth. See superlinear growth.
quadratic replicator
A pattern that fills all or part of the Life
plane by making copies of itself in a nonlinear way. Small quadratic
replicators are known in other Life-like rules, but as of July 2018
no example has been found or constructed in Conway's Life.
quadratic sawtooth
Any sawtooth pattern with a quadratic envelope,
or specifically a pattern assembled by Martin Grant in May 2015,
consisting of two caber tossers with period multipliers for timing
which activate and deactivate two toggleable rake guns (see
toggleable gun). The gliders emitted by those rakes annihilate on
the diagonal while the rakes are eaten by 2c/5 ships. All the rakes
and gliders are destroyed before the next cycle. See also
Osqrtlogt.
quarter
c/4 diagonally, p4
The following spaceship, found by
Jason Summers in September 2000. The name is due to the 25-cell
minimum population. This is the smallest known c/4 spaceship other
than the glider. This spaceship can also be used to make the
smallest known tubstretcher.

quarter diagonal
A unit of measurement sometimes used for diagonal
distances, especially for slow salvo glider lanes. One advantage
of measurement in quarter diagonals is that gliders travel diagonally
at 1qd/tick, so that the same integer value can serve as either a
time or a diagonal distance measurement.
quasar
p3
Found by Robert Wainwright, August 1971. This is related
to the pulsar, and is just the smallest of an extensible series of
p3 oscillators built using pulsar quadrants which are shifted with
respect to each other.
.png)
Here is the next oscillator in the series.
.png)
quasi still life
A stable constellation where the individual
still lifes share dead cells, so the neighborhoods of those dead
cells are changed, but all cells that used to remain dead from
under-population still do so. Under Life rules, this occurs when
objects are diagonally adjacent (e.g., two blocks sharing a single
diagonal neighbor) or when single protruding cells in two objects
such as tubs share multiple neighbors. The term is due to Mark
Niemiec.
----------------
Bits Count
----------------
8 6
9 13
10 57
11 141
12 465
13 1224
14 3956
15 11599
16 36538
17 107415
18 327250
19 972040
20 2957488
21 8879327
22 26943317
----------------
As the number of bits increases, the quasi still life count goes up
exponentially by approximately O(3.04n), slightly more than a factor
of three. By comparison, the rate for strict still lifes is about
O(2.46n) while for pseudo still lifes it's around O(2.56n).
queen bee shuttle
p30
Found by Bill Gosper in 1970. There are a
number of ways to stabilize the ends. Gosper originally stabilized
shuttles against one another in a square of eight shuttles. Two
simpler methods are shown here; for a third see buckaroo. The queen
bee shuttle is the basis of all known true p30 guns (see
Gosper glider gun).

queen bee shuttle pair
Any arrangement of two queen bee shuttles
such that the two beehives created between them are consumed in
some way. There are many ways that the two shuttles can be placed,
either head-to-head, or else at right angles. The most well-known
and useful arrangement results in the Gosper glider gun.
Other arrangements don't create any lasting output, but create
large sparks which can perturb objects (especially gliders) in
various ways. For example, one arrangement of a queen bee shuttle
pair was used in the original unit Life cell as a memory cell.
Here an input glider is converted into a block, which remains until
it is deleted by a glider on a right-angled path.

See p690 gun and metamorphosis II for two more examples.
Quetzal
Any Herschel track-based gun with a period below 62, which is
the lowest period with a stable glider-emitting conduit. This was
Dieter Leithner's name for the true p54 glider gun he built in
January 1998 - a short form of Quetzalcoatlus, which expresses the
fact that the gun was a very large Herschel loop that was not an
emu. Shortly afterwards Leithner also built a p56 Quetzal using a
mechanism found by Noam Elkies for this purpose. In October 1998
Stephen Silver constructed a p55 Quetzal using Elkies' p5 reflector
of the previous month. Quetzals of periods 57-61 have since been
constructed.
Some of the more recent Quetzals are not Herschel loops, but are
instead short Herschel tracks firing several glider streams all but
one of which is reflected back to the beginning of the track to
create a new Herschel. Noam Elkies first had the idea of doing this
for the p55 case, and Stephen Silver constructed the resulting gun
shortly after building the original (much larger) p55 Quetzal. Jason
Summers later built a p54 version, which is more complicated because
the evenness of the period makes the timing problems considerably
more difficult.
Quetzalcoatlus
A giant flying dinosaur after which Dieter Leithner
named his p54 gun. Usually abbreviated to Quetzal, or simply Q (as
in Q54, Q55, Q56, Q-gun, etc.).
R2D2
p8
This was found, in the form shown below, by Peter Raynham
in the early 1970s. The name derives from a form with a larger and
less symmetric stator found by Noam Elkies in August 1994. Compare
with Gray counter.

R64
An elementary conduit, one of the original sixteen
Herschel conduits, discovered by Dave Buckingham in September 1995.
After 64 ticks, it produces a Herschel rotated 90 degrees clockwise
at (11, 9) relative to the input. Its recovery time is 153 ticks,
though this can be improved to 61 ticks by adding a from-the-side
eater inside the turn to avoid interference from the output
Herschel's first natural glider, as shown below. A
ghost Herschel in the pattern below marks the output location:

R64 is one of the simplest known Spartan conduits, one of the two
known Blockic conduits, and one of the few elementary conduits in
the original set of sixteen. See also p256 gun.
rabbits
stabilizes at time 17331
A 9-cell methuselah found by
Andrew Trevorrow in 1986.
.png)
The following predecessor, found by Trevorrow in October 1995, has
the same number of cells and lasts two generations longer.
.png)
racetrack
A pattern in which a signal makes its way in a loop
through an "obstacle course" of reactions in order to demonstrate
various ways that the signal can be reflected, temporarily stored,
and converted. The more different reactions that are used the better
the racetrack. David Goodenough built racetracks for p30 and p46
technology in 1995. Racetracks are also known for
Herschel conduit technology, and simple ones are useful for
building oscillators and glider guns.
rake
Any puffer whose debris consists of spaceships. A rake is
said to be forwards, backwards or sideways according to the direction
of the spaceships relative to the direction of the rake. Originally
the term "rake" was applied only to forwards c/2 glider puffers (see
space rake). Many people prefer not to use the term in the case
where the puffed spaceships travel parallel or anti-parallel to the
puffer, as in this case they do not rake out any significant region
of the Life plane (and, in contrast to true rakes, these puffers
cannot travel in a stream, and so could never be produced by a
gun).
Although the first rakes (circa 1971) were c/2, rakes of other
velocities have since been built. Dean Hickerson's construction of
Corderships in 1991 made it easy for c/12 diagonal rakes to be
built, although no one actually did this until 1998, by which time
David Bell had constructed c/3 and c/5 rakes (May 1996 and September
1997, respectively). Jason Summers constructed a 2c/5 rake in June
2000 (building on work by Paul Tooke and David Bell) and a c/4
orthogonal rake in October 2000 (based largely on reactions found by
David Bell).
The smallest possible period for a rake is probably 7, as this
could be achieved by a 3c/7 orthogonal backwards glider puffer. The
smallest period attained to date is 8 (Jason Summers' backrake,
March 2001).
$rats
p6
Found by Dave Buckingham, 1972.

rattlesnake
p11
Found by Dean Hickerson in January 2016 and named
by Jeremy Tan.

R-bee
= bun. This name is due to the fact that the pattern is a
single-cell modification of a beehive.
reaction envelope
The collection of cells that are alive during
some part of a given active reaction. This term is used for
Herschel circuits and other stable circuitry, whereas
construction envelope is specific to recipes in self-constructing
circuitry.
There are some subtleties at the edges of the envelope.
Specifically, two reactions that have the exact same set of cells
defining their envelopes may have different behavior when placed next
to a single-cell protrusion like the tail of an eater1, or one side
of a tub. The difference depends on whether two orthogonally
adjacent cells at the edge of the envelope are ever simultaneously
alive, within the protruding cell's zone of influence.
reanimation
A reaction performed by a convoy of spaceships (or
other moving objects) which converts a common stationary object into
a glider without harming the convoy. This provides one way for
signals that have been frozen in place by some previous reaction to
be released for use.
Simple reactions using period 4 c/2 spaceships have been found for
reanimating a block, boat, beehive, ship, loaf, bi-block,
or toad. The most interesting of these is for a beehive since it
seems to require an unusual p4 spaceship:

Reanimation of a loaf is used many times in the Caterloopillar.
It is also used in the Caterpillar as part of its catch and throw
mechanism. Finally, reanimation can produce rakes from some
puffers. See stop and restart for a similar idea that applies to
Herschel conduits and other signal circuitry.
There are small objects which have no known reanimation reactions
using c/2 ships other than the brute force method of hitting them
with the output of rakes.
reburnable fuse
A very rare type of fuse whose output is identical
to its input, possibly with some spatial and/or temporal offset. See
lightspeed wire for an example. Reburnable fuses are used
primarily in the construction of fixed-speed self-supporting
macro-spaceships, where the speed of the fuse's burning reaction
becomes the speed of the spaceship. Examples include the
Caterpillar, Centipede, and waterbear.
recovery time
The number of ticks that must elapse after a signal
is sent through a conduit, before another signal can be safely sent
on the same path. In general, a lower recovery time means a more
useful conduit. For example, the Snark's very low recovery time
allowed for the creation of oscillators with previously unknown
periods, 43 and 53.
For the most part this is a synonym for repeat time. However,
overclocking a complex circuit can often allow it to be used at a
repeat time much lower than its safe recovery time.
rectifier
The smallest known 180-degree reflector, discovered by
Adam P. Goucher in 2009. It was the smallest and fastest stable
reflector of any kind until the discovery of the Snark in 2013. The
rectifier has the same output glider as the boojum reflector but a
much shorter repeat time of only 106 ticks.
Another advantage of the rectifier is that the output glider is on
a transparent lane, so it can be used in logic circuitry to merge
two signal paths.

recursive filter
A toolkit developed by Alexey Nigin in July 2015,
which enables the construction of patterns with population growth
that asymptotically matches an infinite number of different
superlinear functions. Toolkits enabling other, sublinear infinite
series had been completed by Dean Hickerson and Gabriel Nivasch in
2006. See quadratic filter and exponential filter.
Sublinear functions are possible using the recursive-filter toolkit
as well. It can be used to construct a glider-emitting pattern with
a slowness rate S(t) = O(log***...*(t)), the nth-level iterated
logarithm of t, which asymptotically dominates any
primitive-recursive function f(t).
reflector
Any stable or oscillating pattern that can reflect some
type of spaceship (usually a glider) without suffering permanent
damage. A pattern that is damaged or destroyed during the reflection
process is generally called a one-time turner instead.
The first known reflector was the pentadecathlon, which functions
as a 180-degree glider reflector (see relay). Other examples
include the buckaroo, the twin bees shuttle and some oscillators
based on the traffic jam reaction. Glider guns can also be made
into reflectors, although these are mostly rather large.
In September 1998 Noam Elkies found some fast small-period glider
reflectors, with oscillators supplying the required domino
sparks at different periods. A figure-8 produced a p8 bouncer,
and a p6 pipsquirter produced an equivalent p6 bouncer. A more
complicated construction allows a p5 bouncer (which, as had been
anticipated, soon led to a true p55 Quetzal gun). And in August
1999 Elkies found a suitable sparker to produce a p7 bouncer,
allowing the first p49 oscillator to be constructed.
These were all called simply "p5 reflector", "p6 reflector", etc.,
until 6 April 2016 when Tanner Jacobi discovered an equally small and
simple reaction, the bumper, starting with a loaf as bait
instead of a boat. This resulted in a series of periodic
colour-preserving reflectors, whereas Elkies' bouncer reflectors
are all colour-changing. A useful mnemonic is that "bouncer"
contains a C and is colour-changing, whereas "bumper" contains a P
and is colour-preserving.
Stable reflectors are special in that if they satisfy certain
conditions they can be used to construct oscillators of all
sufficiently large periods. It was known for some time that stable
reflectors were possible (see universal constructor), but no one
was able to construct an explicit example until Paul Callahan did so
in October 1996.
Callahan's original reflector has a repeat time of 4840, soon
improved to 1686, then 894, and then 850. In November 1996 Dean
Hickerson found a variant in which this is reduced to 747. Dave
Buckingham reduced it to 672 in May 1997 using a somewhat different
method, and in October 1997 Stephen Silver reduced it to 623 by a
method closer to the original. In November 1998 Callahan reduced
this to 575 with a new initial reaction. A small modification by
Silver a few days later brought this down to 497.
In April 2001 Dave Greene found a 180-degree stable reflector with
a repeat time of only 202 (see boojum reflector). This reflector
won bounties offered by Dieter Leithner and Alan Hensel. Half of the
prize money was recycled into a new prize for a small 90-degree
reflector, which in turn was won by Mike Playle's colour-preserving
Snark reflector. The Snark is currently the smallest known stable
reflector, with a recovery time of 43. Playle has offered a $100
prize for a colour-changing stable reflector contained within a 25
by 25 bounding box, with a recovery time of 50 generations or less.
As of June 2018, the following splitter is among the smallest
known 90-degree colour-changing reflectors. The top output can
be blocked off by an eater if needed. For small 180-degree
colour-changing reflectors see rectifier, and also the sample
pattern in splitter.

reflectorless rotating oscillator
A pattern that rotates itself 90 or
180 degrees after some number of generations, with the additional
constraint that multiple non-interacting copies of the pattern can be
combined into a new oscillator with a period equal to the appropriate
fraction of the component oscillators' period. The second constraint
disqualifies small time-symmetric oscillators such as the blinker
and monogram.
A working RRO might look something like a pi orbital or
p256 gun loop containing one or more pis or Herschels in the
same loop, but without any external stabilisation mechanism. Such
patterns can be proven to exist (see universal constructor), but as
of June 2018 none have been explicitly constructed in Life. There is
no upper limit on multiplicity for a constructor-based RRO.
regulator
An object which converts input gliders aligned to some
period to output gliders aligned to a different period. The most
interesting case is a universal regulator, of which several have
been constructed by Paul Chapman and others.
relay
Any oscillator in which spaceships (typically gliders)
travel in a loop. The simplest example is the p60 one shown below
using two pentadecathlons. Pulling the pentadecathlons further
apart allows any period of the form 60+120n to be achieved. This is
the simplest proof of the existence of oscillators of arbitrarily
large period.

repeat time
The minimum number of generations that is possible
between the arrival of one object and the arrival of the next. This
term is used for things such as reflectors or conduits where the
signal objects (gliders or Herschels, for example) will
interact fatally with each other if they are too close together, or
one will interact fatally with a disturbance caused by the other.
For example, the repeat time of Dave Buckingham's 59-step B-heptomino
to Herschel conduit (shown under conduit) is 58.
rephaser
The following reaction that shifts the phase and path of a
pair of gliders. There is another form of this reaction,
glider-block cycle, that reflects the gliders 180 degrees.

replicator
A finite pattern which repeatedly creates copies of
itself. Such objects are known to exist (see
universal constructor), but no concrete example is known. The
linear propagator may be considered to be the first example of a
replicator built in Life, but this is debatable as each of its copies
replicates itself only once, allowing no possibility of
superlinear growth.
reverse caber tosser
A storage mechanism for data feeding a
universal constructor designed by Adam P. Goucher in 2018. A very
large integer can be encoded in the position of a very faraway
object. If the distance to that object is measured using circuitry
designed to be as simple as possible, a complete decoder and
universal constructor can be created by colliding a small number of
gliders - no more than 329 according to a June 2018
glider synthesis, and exactly 43 according to a July 1 redesign by
Chris Cain using eight far-distant GPSEs and, amazingly, no
stationary circuitry except for a single catalyst block. Some
intermediate designs with 50+ gliders need no stationary circuitry at
all.
With the correct placement of the faraway object, the complete
pattern is theoretically capable of building any glider-constructible
object. This means that 43 is the maximum number of gliders required
to build any constructible object, no matter what size. However, it
is not possible to determine in practice what the locations of these
43 gliders should be, even for a relatively simple construction.
reverse fuse
A fuse that produces some initial debris, but then
burns cleanly. The following is a simple example.

revolver
p2

RF28B
A converter with several known forms, many of which found by
Dave Buckingham in 1972 and in the early 1980s. It accepts an
R-pentomino as input and produces an output B-heptomino 28 ticks
later. Of nine major variants known as of July 2018, four versions
are shown below. For each version, the R-pentomino inputs are shown
near the left and right edges, along with the B-heptomino output
locations near the center.

The version in the southeast is used in Paul Callahan's
Herschel receiver. The one in the northwest is part of L156, but
can be replaced by the variant in the northeast which produces a
forward glider output.
RF48H
Stephen Silver's alternate completion of Paul Callahan's
Herschel receiver. As of June 2018 there are four known variants.
The original version consists of a single loaf. A ghost Herschel
marks the output location.

Rich's p16
A period 16 oscillator found by Rich Holmes in July 2016,
using apgsearch. For its use as a filter see for example
p48 gun.

ring of fire
p2
The following muttering moat found by Dean
Hickerson in September 1992.

rle
Run-length encoded. Run-length encoding is a simple (but not
very efficient) method of file compression. In Life the term refers
to a specific ASCII encoding used for patterns in Conway's Life and
other similar cellular automata. This encoding was introduced by
Dave Buckingham and is now the usual means of exchanging relatively
small patterns by email or in online forum discussions.
As an example of the rle format, here is a representation of the
Gosper glider gun. The "run lengths" are the numbers, b's are dead
cells, o's are live cells, and dollar signs signal new lines:
x = 36, y = 9, rule = B3/S23
24bo$22bobo$12boo6boo12boo$11bo3bo4boo12boo$oo8bo
5bo3boo$oo8bo3boboo4bobo$10bo5bo7bo$11bo3bo$12boo!
Over the years RLE format has been extended to handle patterns with
multiple states, neighborhoods, rules, and universe sizes. A
completely different encoding, macrocell format, is used for
repetitive patterns that may have very large populations.
R-mango
A small active reaction, so named because it is a single-cell
modification of a mango, but now more commonly known as dove.
RNE-19T84
The following edge shooter converter, accepting an
input R-pentomino and producing a glider heading northeast (if the
R-pentomino is in standard orientation).
.png)
This converter has several common uses. It can be attached to the
L156 Herschel conduit to change it into a useful
period doubler. Connecting it to the initial stage of the L156
produces a composite Herschel-to-glider converter often used as a
splitter, or as a quasi-edge shooter after suppressing the
additional glider output:
.png)
The above H-to-2G mechanism appears in many places in the glider gun
collection, for example, mainly for periods below 78 where syringes
can't be used to build small true-period guns. The insertion
reaction allows a glider to be placed 19 ticks in front of another
glider on the same lane, or 30 ticks behind it (28 if the
perpendicular glider output is suppressed.)
rock
Dean Hickerson's term for an eater which remains intact
throughout the eating process. The snake in Dave Buckingham's
59-step B-to-Herschel conduit (shown under conduit) is an example.
Other still lifes that sometimes act as rocks include the tub, the
hook with tail, the eater1 (eating with its tail) and the hat
(in Heinrich Koenig's stabilization of the twin bees shuttle).
rotor
The cells of an oscillator that change state. Compare
stator. It is easy to see that any rotor cell must be adjacent to
another rotor cell.
R-pentomino
This is by far the most active polyomino with less than
six cells: all the others stabilize in at most 10 generations, but
the R-pentomino does not do so until generation 1103, by which time
it has a population of 116, including six gliders.

At generation 774, an R-pentomino produces a queen bee which lasts
17 more generations before being destroyed, enough time for it to
flip over. This observation led to the discovery of the
Gosper glider gun.
rule 22
Wolfram's rule 22 is the 2-state 1-D cellular automaton in
which a cell is ON in the next generation if and only if exactly one
of its three neighbours is ON in the current generation (a cell being
counted as a neighbour of itself). This is the behaviour of Life on
a cylinder of width 1.
ruler
A pattern constructed by Dean Hickerson in April 2005 that
produces a stream of LWSS with gaps in it, such that the number of
LWSS between successive gaps follows the "ruler function" (sequence
A001511 in The On-Line Encyclopedia of Integer Sequences).
rumbling river
Any oscillator in which the rotor is connected and
contained in a strip of width 2. The following p3 example is by Dean
Hickerson, November 1994.

salvo
A collection of spaceships, usually gliders, all travelling in
the same direction. Any valid glider construction recipe can be
partitioned into no more than four salvos. Compare flotilla. In
contrast with a convoy, the spaceships in a salvo are usually
consumed by the reactions that they cause. Simple examples include
block pusher and block pull.
Salvos may be slow or synchronized. The following partially
synchronized three-glider salvo produces an LWSS from a block.

The above is a synchronized salvo and not a slow salvo, because the
second glider must follow the first with the exact separation shown.
The third glider can be considered to be a slow glider, because it
will still delete the temporary loaf no matter how many ticks it is
delayed. The slow glider construction entry includes an example of
a true slow salvo.
sawtooth
Any finite pattern whose population grows without bound
but does not tend to infinity. (In other words, the population
reaches new heights infinitely often, but also infinitely often
returns to some fixed value.) Conway's preferred plural is
"sawteeth".
The first sawtooth was constructed by Dean Hickerson in April 1991.
The current smallest known sawtooth was found by a conwaylife.com
forum user with the online handle 'thunk'. It has a bounding box of
74×60, and is the smallest known sawtooth in terms of its minimum
repeating population of 177 cells. The following variant has a higher
repeating population of 194 and an optimized bounding box of 62×56:

Patterns combining a fast puffer with a slower spaceship have
also been constructed (see moving sawtooth). See also
tractor beam.
Schick engine
c/2 orthogonally, p12
This spaceship, found by Paul
Schick in 1972, produces a large spark (the 15 live cells at the
rear in the phase shown below) which can be perturbed by other
c/2 spaceships to form a variety of puffers. See blinker ship
for an example perturbation of the spark. The diagram below shows
the smallest form of the Schick engine, using two LWSS. It is also
possible to use two MWSSes or two HWSSes, or even an LWSS and an
HWSS.
scorpion
p1

scrubber
p2
Found in 1971.

seal
c/6 diagonally, p6
The first diagonal c/6 spaceship, found
by Nicolay Beluchenko in September 2005.

search program
A computer program or script that automates the search
for Life objects having certain desired properties. These are used
because the difficulty of finding previously unknown Life objects now
commonly exceeds the patience, speed, and accuracy of humans.
Various types of search programs are used for finding objects such as
spaceships, oscillators, drifters, catalysts, soups,
Gardens of Eden, and slow salvos.
Some search programs generate partial results as they are
running, so even if they don't complete successfully, something of
use might still be salvaged from the run.
Example search programs are dr, lifesrc, gfind, and
Bellman.
There are other types of programs which don't perform searches as
such, but instead perform large constructions. These are used to
correctly complete very complicated objects such as the
Caterpillar, Gemini, Caterloopillar, and
universal constructor-based spaceships such as the Demonoids and
Orthogonoids.
second glider domain
The second glider domain of an edge shooter is
the set of spacetime offsets, relative to the glider stream
emitted by the edge shooter, where a second independent glider stream
may be present without interfering with the edge shooter. This is
useful to know, because edge shooters are often used to generate
glider streams very close to other glider streams, to make for
example a spaceship gun or converter.
second natural glider
The glider produced at T=72 during the
evolution of a Herschel. This is the common edge-shooting glider
output used in the NW31 converter and several other converter
variants.
seed
A constellation of still lifes and/or oscillators, which can
be converted into another Life object when it is struck by one or
more gliders. Usually the resulting object is a rare still life or
spaceship, more complex than the original constellation. Spartan
single-glider (1G) seeds are more commonly seen than multi-glider
seeds, because a Spartan 1G seed can be readily constructed and
triggered using a slow salvo. See also freeze-dried. For
example, the following is a 14sL 1G seed for a c/7 loafer
spaceship.

Seeds of Destruction Game
An interactive search application written
by Paul Chapman in 2013. Its primary purpose was to assist in the
design of self-destruct circuits in self-constructing circuitry. It
has also regularly been helpful in completing glider syntheses, and
was used to find the 31c/240 base reaction for the shield bug and
Centipede spaceships.
self-constructing
A type of pattern, generally a macro-spaceship,
that contains encoded construction information about itself, and
makes a complete copy of itself using those instructions. The
Gemini, linear propagator, spiral growth patterns, Demonoids
and Orthogonoid are examples of self-constructing patterns.
Self-constructing spaceships often have trivially adjustable speeds.
In many cases, the direction of travel can also be altered, less
easily, by changing the encoded construction recipe. Compare
self-supporting, elementary.
self-supporting
A type of pattern, specifically a macro-spaceship,
that constructs signals or tracks or other scaffolding to assist
its movement, but does not contain complete information about its own
structure. Examples include the Caterpillar, Centipede,
half-baked knightship, waterbear, and the Caterloopillars.
Caterpillar has been used as a general term for self-supporting
spaceships, but it is not very appropriate for the HBKs.
In general a self-supporting pattern cannot be trivially adjusted
to alter its speed or direction. The variable speeds of the HBKs and
the Caterloopillars are exceptions, but their direction of travel is
fixed, and a specific Caterloopillar can't be made to change its
speed without completely rebuilding it. Compare self-constructing,
elementary.
semi-cenark
Either of two semi-Snark variants discovered by Tanner
Jacobi in November 2017. The name is due to the initial converter,
which produces a century output for every two input gliders. The
minimum safe repeat time is 43 ticks for the smaller initial
catalyst shown in CC semi-cenark and CP semi-cenark, or 42
ticks with the slightly larger catalyst variant shown below. There
is also overclocking possible at period 36, 38, or 39. The reset
glider can be followed immediately by a new trigger glider, as shown
below, so the minimum repeat time for an intermittent stream of
gliders is only 50 ticks.

semi-Snark
Any small stable signal conduit that produces one
output glider for every two input gliders, with a 90 degree
reflection. These can act as period-doublers for any glider stream
whose period is at least equal to their repeat time, and so adding
one of these to a single glider gun often results in a pattern much
smaller than the older technology of crossing the output of two
guns.
The available semi-Snarks differ in their complexity, size, repeat
time, and the colour of their output gliders. The CC semi-Snark
was the first one found, and the term "semi-Snark" is often used
specifically for this object. The "CC" prefix stands for
colour-changing, by contrast with the more recently discovered
colour-preserving CP semi-Snark.
There are also CC and CP variants of a semi-Snark based on a
two-glider to century converter discovered by Tanner Jacobi in
November 2017. These semi-cenarks are the fastest semi-Snarks
known as of July 2018, with a repeat time as low as 50 ticks, or a
periodic input rate as low as 36 ticks.
shield bug
31c/240 orthogonally, p240
The first 31c/240
macro-spaceship, constructed by Dave Greene on September 9, 2014.
shillelagh
p1

ship in a bottle
p16
Found by Bill Gosper in August 1994. See also
bottle.

ship-tie
p1
The name is by analogy with boat-tie.

ship tie boat
p1

sidecar
A small tagalong for an HWSS that was found by Hartmut
Holzwart in 1992. The resulting spaceship (shown below) has a
phase with only 24 cells, making it in this respect the smallest
known spaceship other than the standard spaceships and some trivial
two-spaceship flotillas derived from them. Note also that an HWSS
can support two sidecars at once.

sidesnagger
A Spartan eater found by Chris Cain in May 2015 with
functionality similar to the eater5, as shown below. It has one
lane less diagonal clearance on the high-clearance side than
other eater5 variants, due to the presence of the boat. A good use
of the sidesnagger can be seen in p130 shuttle. See also
highway robber.

sidewalk
p1

siesta
p5
Found by Dave Buckingham in 1973. Compare sombreros.

signal
Movement of information through the Life universe. Signals
can be carried by spaceships, fuses, drifters, or conduits.
Spaceships can only transfer a signal at the speed of the spaceship,
while fuses can transfer a signal at speeds up to the
speed of light.
In practice, many signals are encoded as the presence or absence of
a glider or other spaceship at a particular point at a particular
time. Such signals can be combined by the collision of gliders to
form logic operations such as AND, OR, and NOT gates. Signals can be
duplicated using glider duplicators or other fanout devices, and
can be used up by causing perturbations on other parts of the Life
object.
Signals are used in Herschel conduit circuitry,
universal constructors, macro-spaceships, and other computational
patterns such as the pi calculator and Osqrtlogt patterns.
signal elbow
A conduit with signal output 90 degrees from its
input. This term is commonly used only for signal wires,
particularly 2c/3 signals. A Snark could reasonably be called a
"glider elbow", but glider reflector is the standard term. A
signal elbow with a recovery time less than 20 ticks would enable a
trivial proof that Conway's Life is omniperiodic.
A near miss is the following elbow-like converter found by Dean
Hickerson. It successfully turns a 2c/3 signal by 90 degrees, but
unfortunately changes it to a double-length signal in the process.
This means that further copies of the converter can not be appended
(e.g., to make a closed loop).

Relatively small composite MWSS elbows can now be constructed,
using Tanner Jacobi's 2015 discovery of a small H-to-MWSS
component. For example, the Orthogonoid includes a
constructor/reflector that reflects an MWSS stream by 180 degrees,
but it can be trivially reconfigured to make a 90-degree MWSS elbow.
Silver G-to-H
A variant of the Silver reflector made by
substituting an Fx119 conduit for the final NW31, allowing a
Herschel output as well as the beehive-annihilating reset glider. It
is still Spartan, and as long as the Fx119 is followed by a
dependent conduit, it retains the faster 497-tick recovery time.
Silver reflector
A stable glider reflector found by Stephen
Silver in November 1998, by substituting an NW31 converter for the
second Fx77 conduit in the Callahan G-to-H found a few days
previous. The repeat time is 497 ticks:

Silver's p5
p5
The following oscillator found by Stephen Silver in
February 2000:
As this has no spark, it appears useless. Nonetheless, in March
2000, David Eppstein found a way to use it to reduce the size of Noam
Elkies' p5 reflector.
Simkin glider gun
p120
A Herschel-based glider gun discovered by
Michael Simkin in April 2015. It consists of a Herschel running
through two B60 conduits. In terms of its 36-cell minimum
population, it is one of the smallest known guns, sharing the record
with the Gosper glider gun. In the double-barreled form, as well as
the pseudo-period, snake-stabilized form shown below, it is the
absolute record holder.

single-channel
A type of universal constructor discovered and
developed by Simon Ekström and others starting in December 2015. The
initial elbow operation toolkit was near-minimal, with just one
push, one pull, and one output glider of each colour (see
colour of a glider). Later searches produced a much larger and
more efficient library.
Single-channel recipes consist of a stream of gliders on a
single lane and aimed at a construction elbow, usually separated
from each other by at least 90 ticks. In spite of these strict
limitations, single-channel recipes can be made to do surprising
things. For example, it is possible to build a Snark directly on
the construction lane of an active construction arm, starting from
a single elbow block. This can allow the arm to reach
efficiently around complex obstructions by bending itself through
multiple lossless elbows. Known recipes can also remove an elbow
when it is no longer needed, by controlled demolition of the Snark.
As of June 2018, almost all single-channel recipes are made up of
singletons and synchronized pairs of gliders, but no synchronized
triplets or larger groups. This is not an inherent limitation of
single-channel construction, but rather a limitation in the
search program used to find currently known single-channel
toolkits.
A useful byproduct of this limitation is that single-channel
recipes can be trivially adjusted to allow them to safely cross
perpendicular data streams, including other single-channel recipes
(or earlier parts of the same recipe). To avoid collisions with a
crossing stream, each singleton glider or glider pair can safely be
delayed by any even number of ticks, or technically by any multiple
of the period of the current intermediate target. The final result
of the construction will not be affected.
singular flip flop
p2
Found by Robert Wainwright, July 1972.

Sir Robin
(2,1)c/6, p6
The first elementary knightship in
Conway's Game of Life, found by Adam P. Goucher on March 6, 2018,
based on a partial by Tomas Rokicki.

sixty-nine
p4
Found by Robert Wainwright, October 1978.

skewed quad
p2

skewed traffic light
p3
Found by Robert Wainwright, August 1989.

sL
Abbreviation for still life, used most often in rough
measurements of the complexity of a Spartan constellation.
slide gun
A gun which fires sideways from an extending arm. The
arm consists of streams of spaceships which are pushing a pattern
away from the body of the gun and releasing an output spaceship every
time they do so. Each output spaceship therefore travels along a
different path.
Dieter Leithner constructed the first slide gun in July 1994
(although he used the term "side shooting gun"). The following
pattern shows the key reaction of this slide gun. The three gliders
shown will push the block one cell diagonally, thereby extending the
length of the arm by one cell, and at the same time they release an
output glider sideways. (In 1999, Jason Summers constructed slide
guns using other reactions.)

sliding block memory
A memory register whose value is stored as the
position of a block. The block can be moved by means of glider
collisions. See block pusher for an example.
In Conway's original formulation (as part of his proof of the
existence of a universal computer in Life) two gliders were used to
pull the block inwards by three diagonal spaces, as shown below, and
thirty gliders were used to push it out by the same amount.

Dean Hickerson later greatly improved on this, finding a way to
pull a block inwards by one diagonal space using 2 gliders, and push
it out the same distance using 3 gliders. In order for the memory to
be of any use there also has to be a way to read the value held. It
suffices to be able to check whether the value is zero (as Conway
did), or to be able to detect the transition from one to zero (as
Hickerson did).
Dean Hickerson's sliding block memory is used in Paul Chapman's
URM, and the key salvos from it are used in several other complex
constructions, such as David Bell's Collatz 5N+1 simulator and Adam
P. Goucher's pi calculator and Spartan
universal computer-constructor.
slow elbow
A movable construction elbow that is controlled by a
slow salvo, which most likely comes from a previous elbow in a
multi-elbow construction arm. Unlike a standard elbow which is
generally fixed on a single construction lane or at least within a
narrow range, a slow elbow can move freely in two dimensions as long
as there is room for it. Each slow elbow added to a construction arm
results in an exponential increase in the cost (in gliders) of the
final construction. Compare lossless elbow.
slow glider construction
Construction an object by a "slow salvo" of
gliders all coming from the same direction, in such a way that
timing of the gliders does not matter as long as they are not too
close behind one another. This type of construction requires an
initial seed object, such as a block, which is modified by each
glider in turn until the desired object is produced.
In May 1997, Nick Gotts produced a slow glider construction of a
block-laying switch engine from a block, using a slow salvo of 53
gliders. Constructions like this are important in the study of
sparse Life, as they will occur naturally as gliders created in the
first few generations collide with blonks and other debris.
Slow glider constructions are also useful in some designs for
universal constructors. However, in this case the above definition
is usually too restrictive, and it is desirable to allow
constructions in which some gliders in the salvo are required to have
a particular timing modulo 2 (a "p2 slow salvo"). This gives much
greater flexibility, as blinkers can now be freely used in the
intermediate construction steps. The Snarkmaker is a very large p2
slow salvo. A much smaller example is the following edgy
construction of an eater1 starting from a block.

Adam P. Goucher's slmake search program, made available in May
2017, makes it much easier to find a slow glider construction for a
wide variety of stable circuitry.
small lake
p1
A 20-cell still life, but technically not actually
a lake because it is not constructed entirely out of dominoes.

smiley
p8
Found by Achim Flammenkamp in July 1994 and named by Alan
Hensel.

smoke
Debris that is fairly long-lived but eventually dies
completely. Basically, a large spark. This term is used
especially when talking about the output from a smoking ship. Some
Herschel conduits such as Fx119 also create large amounts of
smoke.
smoking ship
A spaceship which produces smoke. If the smoke
extends past the edge of the rest of the spaceship, then it can be
used to perturb other objects as the spaceship passes by. Running
gliders into the smoke is often a good way to turn or duplicate them,
or convert them into other objects. Sometimes the smoke from a
smoking ship may itself be perturbed by accompanying spaceships in
order to form a puffer. A simple example of a smoking ship is the
Schick engine.
snacker
p9
Found by Mark Niemiec in 1972. This is a
pentadecathlon with stabilizers which force it into a lower period.
.png)
The stabilizers make the domino spark largely inaccessible, but the
snacker is extensible, as shown in the next diagram, and so a more
accessible p9 domino spark can be obtained. In April 1998 Dean
Hickerson found an alternative stabilizer that is less obtrusive than
the original one, and this is also shown in this diagram.
.png)
An end can also be stabilized by killer candlefrobras.
snail
c/5 orthogonally, p5
The first known c/5 spaceship,
discovered by Tim Coe in January 1996. For some time it was the
slowest known orthogonal spaceship.

snake
p1

snake bit
An alternative name for a boat-bit. Not a very sensible
name, because various other things can be used instead of a snake. A
snake, or alternatively an aircraft carrier, is the smallest object
that can consume a glider stream by effectively acting as an
eater for every two incoming gliders. The one-cell reduction from
the smallest real eater, the seven-cell eater1, has been important
when trying to construct recent sawtooths where the population
must be minimized.
snake bridge snake
p1

snake dance
p3
Found by Robert Wainwright, May 1972.

snake pit
This term has been used for two different oscillators:
the p2 snake pit (essentially the same as fore and back)
.png)
and the p3 snake pit.
.png)
snake siamese snake
p1

Snark
A small stable 90-degree glider reflector with a repeat time of
43 ticks, discovered by Mike Playle on 25 April 2013 using a search
utility he wrote called Bellman. Compare boojum reflector. Four
common Snark variants are shown below: Playle's original at the top,
and variants by Heinrich Koenig, Simon Ekström, and Shannon Omick to
the left, bottom, and right, respectively. As of June 2018, only
Playle's variant has a known slow glider construction recipe for
all orientations.

sombreros
p6
Found by Dave Buckingham in 1972. If the two halves
are moved three spaces closer to one another then the period drops to
4, and the result is just a less compact form of Achim's p4.
Compare also siesta.

soup
A random initial pattern, either contained within a small area,
or alternatively filling the whole Life universe.
Finite soups probably have behaviors very different than infinite
soups, but this is obviously unknown. Infinite soups may remain
chaotic indefinitely since any reaction, no matter how rare, is bound
to happen somewhere.
Soups can have an average density, with results varying based on
that. See sparse Life for a discussion of what can happen at a low
density.
Finite soups for sizes such as 16×16 (asymmetric) have been
examined by the billions by scripts such as apgsearch to find
interesting results. Many new oscillators and synthesis
recipes have been discovered, as well as previously known rare
patterns such as stabilized switch engines. In addition, soups are
used to generate statistical census data, and to decide whether
specific objects can be considered natural.
Soups can be fully random, or they can be forced to be symmetric.
The results for these two types of soups can differ since symmetric
soups tend to create large symmetrical objects at a much higher rate.
Shown below is an unusual mirror-symmetric soup that produces a
pufferfish and nothing else.

space dust
A part of a spaceship or oscillator which looks like a
random mix of ON and OFF cells. It is usually very difficult to find
a glider synthesis for an object that consists wholly or partly of
space dust. As examples, the 295P5H1V1, fly, and seal
spaceships contain large amounts of space dust.
spacefiller
Any pattern that grows at a quadratic rate by filling
space with an agar. The first example was found in September 1993
by Hartmut Holzwart, following a suggestion by Alan Hensel. The
diagram below shows a smaller spacefiller found by Tim Coe. See also
Max. Spacefillers can be considered as breeders (more precisely,
MMS breeders), but they are very different from ordinary breeders.
The word "spacefiller" was suggested by Harold McIntosh and soon
became the accepted term.

space nonfiller
Any pattern that expands indefinitely to affect every
cell in the Life plane, but leaves an expanding region of vacuum at
its center. Compare spacefiller; see also antstretcher. The
first nonfiller was discovered by Jason Summers on 14 April 1999:

space rake
The following p20 forwards glider rake, which was the
first known rake. It consists of an ecologist with a LWSS added
to turn the dying debris into gliders.
spaceship
Any finite pattern that reappears (without additions or
losses) after a number of generations and displaced by a non-zero
amount. By far the most natural spaceships are the glider,
LWSS, MWSS and HWSS, followed by the Coe ship which has also
evolved multiple times from random asymmetric soup starting
conditions. See also the entries on individual spaceship speeds:
c/2 spaceship, c/3 spaceship, c/4 spaceship, c/5 spaceship,
c/6 spaceship, c/7 spaceship, c/10 spaceship, c/12 spaceship,
2c/5 spaceship, 2c/7 spaceship, 3c/7 spaceship,
(2,1)c/6 spaceship, and 17c/45 spaceship.
It is known that there exist spaceships travelling in all rational
directions and at arbitrarily slow speeds (see
universal constructor). Before 1989, however, the only known
examples travelled at c/4 diagonally (gliders) or c/2 orthogonally
(everything else).
In 1989 Dean Hickerson started to use automated searches to look
for new elementary spaceships, and had considerable success. Other
people have continued these searches using tools such as lifesrc
and gfind, and as a result we now have a great variety of
elementary spaceships travelling at sixteen different velocities.
The following table details the discovery of elementary spaceships
with new velocities as of July 2018.
-----------------------------------------------------------------
Speed Direction First Discovery Discoverer Date
-----------------------------------------------------------------
c/4 diagonal glider Richard Guy 1970
c/2 orthogonal LWSS John Conway 1970
c/3 orthogonal 25P3H1V0.1 Dean Hickerson Aug 1989
c/4 orthogonal 119P4H1V0 Dean Hickerson Dec 1989
c/12 diagonal Cordership Dean Hickerson Apr 1991
2c/5 orthogonal 44P5H2V0 Dean Hickerson Jul 1991
c/5 orthogonal snail Tim Coe Jan 1996
2c/7 orthogonal weekender David Eppstein Jan 2000
c/6 orthogonal dragon Paul Tooke Apr 2000
c/5 diagonal 295P5H1V1 Jason Summers Nov 2000
c/6 diagonal seal Nicolay Beluchenko Sep 2005
c/7 diagonal lobster Matthias Merzenich Aug 2011
c/7 orthogonal loafer Josh Ball Feb 2013
c/10 orthogonal copperhead zdr Mar 2016
3c/7 orthogonal spaghetti monster Tim Coe Jun 2016
(2,1)c/7 oblique Sir Robin Adam P. Goucher Mar 2018
-----------------------------------------------------------------
Several infinite families of adjustable-velocity macro-spaceships
have also been constructed, of which the first was Gabriel Nivasch's
Caterpillar from December 2004. The macro-spaceship with the
widest range of possible speeds is Michael Simkin's Caterloopillar
from April 2016; in theory it supports any rational orthogonal speed
strictly less than c<4. A somewhat similar design supporting any
rational speed strictly less than c/2 has been shown to be feasible,
but as of July 2018 no explicit examples have been constructed.
A period p spaceship that displaces itself (m,n) during its period,
where m>=n, is said to be of type (m,n)/p. It was proved by Conway
in 1970 that p>=2m+2n. (This follows immediately from the
easily-proved fact that a pattern cannot advance diagonally at a rate
greater than one half diagonal step every other generation.)
Spaceships in Conway's Life
A series of articles posted by David Bell
to the newsgroup comp.theory.cell-automata during the period
August-October 1992 that described many of the new spaceships found
by himself, Dean Hickerson and Hartmut Holzwart. Bell produced an
addendum covering more recent developments in 1996.
spaghetti monster
The first 3c/7 spaceship, found by Tim Coe in
June 2016. The spaceship travels orthogonally, has a minimum of 702
live cells and fits in a 27×137 bounding box.
spark
A pattern that dies. The term is typically used to describe a
collection of cells periodically thrown off by an oscillator or
spaceship, but other dying patterns, particularly those consisting
or only one or two cells (such as produced by certain glider
collisions, for example), are also described as sparks. For examples
of small sparks see unix and HWSS. Examples of much larger
sparks are seen in Schick engine and twin bees shuttle spark.
spark coil
p2
Found in 1971.

sparking eater
One of two eaters found in April 1997 and November
1998 by Dean Hickerson using his dr search program, shown below
to the left and right respectively. These both absorb gliders as a
standard eater does, but also produce separated single-bit sparks
at the upper right, which can be used to delete antiparallel gliders
with different phases as shown.

The above mechanisms can be used to build intermitting glider guns.
The left-hand eater produces a spark nine ticks after a glider
impact, with the result that the period of the constituent guns can't
be a multiple of 4. The right-hand eater produces the same spark ten
ticks after impact, which allows p4N guns to be used.
The separation of the spark also allows this reaction to perform
other perturbations "around the corner" of some objects. For
example, it was used by Jason Summers in 2004 to cap the ends of a
row of ten AK47 reactions to form a much smaller period 94 glider
gun than the original one. (This is now made obsolete by the
AK94 gun.)
sparse Life
This refers to the study of the evolution of a Life
universe which starts off as a random soup of extremely low
density. Such a universe is dominated at an early stage by blocks
and blinkers (often referred to collectively as blonks) in a
ratio of about 2:1. Much later it will be dominated by simple
infinite growth patterns (presumably mostly switch engines). The
long-term fate of a sparse Life universe is less certain. It may
possibly become dominated by self-reproducing patterns (see
universal constructor), but it is not at all clear that there is
any mechanism for these to deal with all the junk produced by switch
engines.
Spartan
A pattern composed of subunits that can be easily constructed
in any orientation, usually with a slow salvo. Generally this means
that the pattern is a constellation of Spartan still lifes:
block, tub, boat, hive, ship, loaf, eater1, or pond.
Other small objects may sometimes be counted as Spartan, including
period-2 oscillators - mainly blinkers, but also beacons or
toads, which may occur as intermediate targets in slow salvo
recipes. Most self-constructing patterns are Spartan or mostly
Spartan, to simplify the process of self-construction.
speed booster
Any mechanism which allows a signal (indicated by the
presence or absence of a spaceship) to move faster than the spaceship
could travel through empty space. The original speed booster is
based on p30 technology, and is shown below:

Here the top glider is boosted by passing through two
inline inverters, emerging 5 cells further along than the unboosted
glider at the left.
The fastest speed boosters are the telegraph and p1 telegraph,
which can transfer a orthogonal signal at the speed of light,
although their bit rate is rather slow.
Diagonal speed boosters have also been built using 2c/3 wires or
other stable components. See stable pseudo-Heisenburp.
The star gate seems like it can transfer a signal faster than the
speed of light. The illusion is explained in
Fast Forward Force Field.
speed of light
The greatest speed at which any effect can propagate;
in Life, a speed of one cell per generation. Usually denoted c.
S-pentomino
Conway's name for the following pentomino, which
rapidly dies.

spider
c/5 orthogonally, p5
This is the smallest known c/5
spaceship, and was found by David Bell in April 1997. Its side
sparks have proved very useful in constructing c/5 puffers,
including rakes. See also PPS.
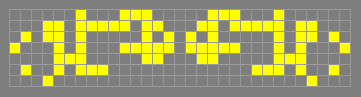
spiral
p1
Found by Robert Wainwright in 1971.

spiral growth
A self-constructing pattern built by Dave Greene in
August 2014 that uses four universal constructors (UCs) arranged in
a diamond to build four more UCs in a slightly larger diamond. This
was the first B3/S23 pattern that exhibited spiral growth. Much
smaller versions have now been constructed using the single-channel
construction toolkit.
splitter
A signal converter that accepts a single input signal
and produces two or more output signals, usually of the same type as
the input. An older term for this is fanout, or "fanout device".
A sub-category is the one-time splitter, which is not technically
a converter because it can only be used once. One-time splitters are
usually small constellations that produce two or more clean
gliders when struck by a single glider. In other words, they are
multi-glider seeds. These are important for constructing
self-destruct circuitry in self-constructing spaceships.
The following combination, a syringe attached to an SE7T14
converter combined with an NW31 converter, is one of the smallest
known glider splitters as of July 2018. Another small splitter with
a 90-degree colour-changing output is shown under reflector.

SPPS
c/5 orthogonally, p30
The symmetric PPS. The original PPS
found by David Bell in May 1998. Compare APPS.
squaredance
The p2 agar formed by tiling the plane with the
following pattern. Found by Don Woods in 1971.

stabilized switch engine
A single switch engine which survives
indefinitely by interacting with the appropriate exhaust such that
it prevents the engine from ever being destroyed.
The only known types of stabilized switch engines were found by
Charles Corderman soon after he discovered the switch engine itself.
There is a p288 block-laying type (the more common of the two) and
the p384 glider-producing type. These two puffers are the most
natural infinite growth patterns in Life. As of June 2018 they are
the basis for every infinite growth pattern ever seen to occur from a
random asymmetric soup, even after trillions of census results by
apgsearch and similar projects.
Patterns giving rise to block-laying switch engines can be seen
under infinite growth, and one giving rise to a glider-producing
switch engine is shown under time bomb.
Here is the block-laying type showing its distinctive zig-zag trail
of blocks.

stable
A pattern is said to be stable if it is a parent of itself.
Stable objects are oscillators with period 1 (p1), and are generally
called still lifes.
stable pseudo-Heisenburp
A multi-stage converter constructed by
Dave Greene in January 2007, using a complex recipe found by Noam
Elkies to insert a signal into a 2c/3 wire. The wire's high
transmission speed allows a signal from a highway robber to catch
up to a salvo of gliders. Ultimately the mechanism restores the
key glider, which was destroyed by the highway robber in the first
stage of the converter, to its exact original position in the salvo.
Much smaller stable pseudo-Heisenburp devices have since been
designed that use simple 0-degree glider seed constellations
instead of a 2c/3 wire.
These patterns are labeled "pseudo-Heisenburp", because a true
Heisenburp device does not even temporarily damage or affect a
passing glider, yet can still produce an output signal in response.
However, it is impossible to construct a stable device that can
accomplish this for gliders. True stable Heisenburp devices are
possible with many other types of spaceships, but not with gliders
which have no usable side sparks to initiate an output signal.
staged recovery
A type of signal-processing circuit where the
initial reaction between catalysts an incoming signal results in an
imperfect recovery. A catalyst is damaged, destroyed completely as
in a bait reaction, or one or more objects are left behind that
must be cleaned up before the circuit can be reused. In any of these
three cases, output signals from the circuit must be used to complete
the cleanup. In theory the cleanup process might itself be dirty,
requiring additional cleanup stages. In rare cases this might
theoretically allow the construction of special-purpose circuits with
a lower recovery time than would otherwise be possible, but in
practice this kind of situation does not commonly arise.
An example is the record-breaking (at the time) 487-tick reflector
constructed by Adam P. Goucher on 12 April 2009. 487 ticks was a
slight improvement over the repeat time of the Silver reflector.
The reflector featured a standard Callahan G-to-H, with cleanup by
an internal dirty glider reflector found by Dieter Leithner many
years before. This in turn was cleaned up by the usual ungainly
Herschel plumbing attached to the G-to-H's output. The dirty glider
reflector is not actually fully recovered before a second p487 signal
enters the full reflector. However, it has been repaired by the time
the internal reflector is actually needed again, so the cycle can be
successfully repeated at p487 instead of p497.
stamp collection
A collection of oscillators (or perhaps other Life
objects) in a single diagram, displaying the exhibits much like
stamps in a stamp album. The classic examples are by Dean Hickerson
(see http://conwaylife.com/ref/DRH/stamps.html).
Many stamp collections contain "fonts" made of single cells (which
cleanly die) to annotate the objects or to draw boxes around them.
For example, here is a stamp collection which shows all the ways that
two gliders can create a loaf or an eater:

Alternatively, stamp collections can use LifeHistory for their
annotations, but this requires a more sophisticated Life program to
handle. Numbers, or more rarely letters, are sometimes constructed
from stable components such as blocks or snakes, but their
readability is somewhat limited by placement constraints.
star
p3
Found by Hartmut Holzwart, February 1993.
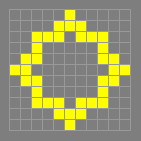
stator
The cells of an oscillator that are always on. Compare
rotor. (The stator is sometimes taken to include also some of
those cells which are always off.) The stator is divided into the
bushing and the casing.
By analogy, the cells of an eater that remain on even when the
eater is eating are considered to constitute the stator of the eater.
This is not always well-defined, because an eater can have more than
one eating action.
statorless
A statorless oscillator is one in which no cell is
permanently on - that is, the stator is empty, or in other words
the oscillator has the maximum possible volatility. See the
volatility entry for examples of this type of oscillator at
different periods. Statorless oscillators can be constructed for any
sufficiently large period, using universal constructor technology.
step
Another term for a generation or tick. This term is
particularly used in describing conduits. For example, a 64-step
conduit is one through which the active object takes 64 generations
to pass.
stillater
p3
Found by Robert Wainwright, September 1985. This is
one of only three essentially different p3 oscillators with only
three cells in the rotor. The others are 1-2-3 and cuphook.

still life
Any stable pattern, usually assumed to be finite and
nonempty. For the purposes of enumerating still lifes this
definition is, however, unsatisfactory because, for example, any pair
of blocks would count as a still life, and there would therefore be
an infinite number of 8-bit still lifes.
For this reason a stricter definition is often used, counting a
stable pattern as a strict still life only if its islands cannot
be divided into two or more nonempty sets both of which are stable in
their own right. If such a subdivision can be made, the pattern can
be referred to as a constellation. If its cells form a single
cluster it is also, more specifically, either a pseudo still life
or a quasi still life.
In rare cases above a certain size threshold, a pattern may be
divisible into three or four stable nonempty subsets but not into
two. See the 32-bit triple pseudo (32 bits) and the 34-bit
quad pseudo for examples.
All still lifes up to 18 bits have been shown to be
glider constructible. It is an open question whether all still
lifes can be incrementally constructed using glider collisions. For
a subset of small still lifes that have been found to be especially
useful in self-constructing circuitry, see also Spartan.
The smallest still life is the block. Arbitrarily large still
lifes are easy to construct, for example by extending a canoe or
barge. The maximum density of a large still life is 1/2, which can
be achieved by an arbitrarily large patch of zebra stripes or
chicken wire, among many other options. See density for more
precise limits.

still life tagalong
A tagalong which takes the form of a
still life in at least one phase. An example is shown below.

stop and go
A pattern by Dean Hickerson in which a period 46
shuttle converts a glider into a block on one oscillation, and then
converts the block back into a glider on the next oscillation. The
glider is reflected back onto its own path, but with a delay.

stop and restart
A type of signal circuit where an input signal
is converted into a stationary object, which is then re-activated by
a secondary input signal. This can be used either as a memory device
storing one bit of information, or as a simple delay mechanism. In
the following January 2016 example by Martin Grant, a
ghost Herschel marks the output signal location, and a "ghost
beehive" marks the location of the intermediate still life.

The eater1 in the lower left corner catches the restart glider if
no input signal has come in to create the beehive. This eater could
be removed if it is useful to have both a "0" and a "1" output for a
memory cell mechanism.
The catch and throw technology in a Caterpillar is a somewhat
similar idea. See also stop and go and reanimation.
stream
A line of identical objects (usually spaceships), each of
which is moving in a direction parallel to the line, generally on the
same lane. In many uses the stream is periodic. For example, the
new gun produces a period 46 glider stream. The stream produced
by a pseudo-random glider generator can have a very high period.
Compare with wave. See also single-channel for a common use of
non-periodic glider streams.
strict still life
A still life that is either a single connected
polyplet, or is arranged such that a stable smaller pattern
cannot be formed by removing one or more of its islands. For
example, beehive with tail is a strict still life because it is
connected, and table on table is a strict still life because
neither of the tables are stable by themselves. See also
triple pseudo, quad pseudo.
Still lifes have been enumerated by Conway (4-7 bits), Robert
Wainwright (8-10 bits), Dave Buckingham (11-13 bits), Peter Raynham
(14 bits), Mark Niemiec (15-24 bits), and Simon Ekström and Nathaniel
Johnston (25-32 bits). The resulting figures are shown below; see
also https://oeis.org/A019473. The most recent search by Nathaniel
Johnston has also confirmed that the triple pseudo pattern found by
Gabriel Nivasch is the only such still life with 32 bits or less. It
is therefore included in the pseudo still life count and not in the
table below.
--------------
Bits Number
--------------
4 2
5 1
6 5
7 4
8 9
9 10
10 25
11 46
12 121
13 240
14 619
15 1353
16 3286
17 7773
18 19044
19 45759
20 112243
21 273188
22 672172
23 1646147
24 4051711
25 9971377
26 24619307
27 60823008
28 150613157
29 373188952
30 926068847
31 2299616637
32 5716948683
--------------
As the number of bits increases, the strict still life count goes
up exponentially by approximately O(2.46n). By comparison, the rate
for pseudo still life}s is about O(2.56n) while for
quasi still lifes it's around O(3.04n).
strict volatility
A term suggested by Noam Elkies in August 1998 for
the proportion of cells involved in a period n oscillator which
themselves oscillate with period n. For prime n this is the same as
the ordinary volatility. Periods with known strictly-volatile
oscillators include 1, 2, 3, 5, 6, 8, 13, 15, 22, 30, 33, and 177.
Examples include figure-8, Kok's galaxy, smiley, and
pentadecathlon. A composite example is the following p22, found by
Nicolay Beluchenko on 4 March 2009:

superfountain
p4
A p4 sparker which produces a 1-cell spark that
is separated from the rest of the oscillator by two clear rows of
cells. The first superfountain was found by Noam Elkies in February
1998. In January 2006 Nicolay Beluchenko found the much smaller one
shown below. See also fountain.

superlinear growth
Growth faster than any rate proportional to T,
where T is the number of ticks that a pattern has been run. This
term usually applies to a pattern's population growth, rather than
diametric growth or bounding-box growth. For example, breeders'
and spacefillers' population asymptotically grows faster than any
linear-growth pattern. It may also be used to describe the rate of
increase in the number of subpatterns present in a pattern, such as
when describing a replicator's rate of reproduction. Due to limits
enforced by the speed of light, no pattern's population can grow at
an asymptotic rate faster than quadratic growth. See
switch-engine ping-pong for the lowest-population superlinear
growth pattern as of July 2018, along with a list of the
record-holders.
superstring
An infinite orthogonal row of cells stabilized on one
side so that it moves at the speed of light, often leaving debris
behind. The first examples were found in 1971 by Edward Fitzgerald
and Robert Wainwright. Superstrings were studied extensively by
Peter Rott during 1992-1994, and he found examples with many
different periods. (But no odd periods. In August 1998 Stephen
Silver proved that odd-period superstrings are impossible.)
Sometimes a finite section of a superstring can be made to run
between two tracks ("waveguides"). This gives a fuse which can be
made as wide as desired. The first example was found by Tony
Smithurst and uses tubs. (This is shown below. The superstring
itself is p4 with a repeating section of width 9 producing one
blinker per period and was one of those discovered in 1971. With the
track in place, however, the period is 8. This track can also be
used with a number of other superstrings.) Shortly after seeing this
example, in March 1997 Peter Rott found another superstring track
consisting of boats. At present these are the only two waveguides
known. Both are destroyed by the superstring as it moves along. It
would be interesting to find one that remains intact.
See titanic toroidal traveler for another example of a
superstring.

support
Those parts of an object which are only present in order to
keep the rest of the object (such an engine or an edge spark)
working correctly. These can be components of the object, or else
accompanying objects used to perturb the object. In many cases
there is a wide variation of support possible for an engine. The
arms in many puffers are an example of support.
surprise
p3
Found by Dave Buckingham, November 1972.

SW1T43
A Herschel-to-glider converter that produces a
tandem glider useful in the tee reaction. It is classified as a
"G3" converter because its two gliders are three lanes apart.

Besides the southwest-travelling glider on lane 1, the converter also
emits the Herschel's standard first natural glider, SW-2. The
converter's full standard name is therefore "HSW1T43_SW-2T21". See
NW31 for an explanation of H-to-G naming conventions.
SW-2
The simplest type of H-to-G converter, where the converter's
effect is simply to suppress a Herschel cleanly after allowing its
first natural glider to escape. The name should be read as "SW
minus two", where -2 is a glider lane number. The complete
designation is SW-2T21. See NW31T120 for a discussion of the
standard naming conventions used for these converters.
An unlimited number of converters have the SW-2T21 classification.
The variants most often used consist of just one or two small
still life catalysts.

swan
c/4 diagonally, p4
A diagonal spaceship producing some
useful sparks. Found by Tim Coe in February 1996.

switch
A signal-carrying circuit that can send output signals to
two or more different locations, depending on the state of the
mechanism. These may be toggle circuits, where the state of the
switch changes after each use, or permanent switches that retain
the same state through many uses until a change is made with a
separate signal.
More generally, any circuit may be referred to as a switch, if it
can alter its output based on stored information. For example, the
following simple mechanism based on an eater2 was discovered by
Emerson J. Perkins in 2007. It either reflects or absorbs an
incoming signal, depending on the presence or absence of a nearby
block. The block is removed if a reflection occurs.

The switching signal here is a glider produced by a high-clearance
syringe variant found by Matthias Merzenich. The syringe is not
technically part of the switch mechanism; any standard Herschel
source can deliver the signal to the block factory (the two
eater1s on the right side of the pattern). Alternate converter
mechanisms could also be used to place the block.
An earlier example of the same type of one-time switch mechanism,
also mediated by a block, can be found in the NW34T204 H-to-G. See
also bistable switch for a very robust and versatile toggle switch
with two input lanes and four possible outputs.
switchable gun
A gun that includes a mechanism to turn the output
stream off and on with simple signals, often gliders. A small
example is Dieter Leithner's switchable LWSS gun from July 8, 1995.
The ON signal enters from the northeast, and the OFF signal from the
northwest:

switch engine
The following pattern discovered by Charles Corderman
in 1971, which is a glide symmetric unstable puffer which moves
diagonally at a speed of c/12 (8 cells every 96 generations).
.png)
The exhaust is dirty and unfortunately catches up and destroys
the switch engine before it runs 13 full periods. Corderman found
several ways to stabilize the switch engine to produce puffers,
using either one or two switch engines in tandem. See
stabilized switch engine and ark.
No spaceships were able to be made from switch engines until Dean
Hickerson found the first one in April 1991 (see Cordership).
Switch engine technology is now well-advanced, producing many c/12
diagonal spaceships, puffers, and rakes of many periods.
Small polyominoes exist whose evolution results in a switch
engine. See nonomino switch engine predecessor.
Several three-glider collisions produce dirty reactions that
produce a stabilized switch engine along with other ash, making
infinite growth. Until recently the only known syntheses for
clean unstabilized switch engines used four or more gliders. There
are several such recipes. In the reaction shown below no glider
arrives from the direction that the switch engine will travel to,
making it easier to repeat the reaction:
.png)
Running the above for 20 ticks completes a kickback reaction with
the top two gliders, resulting in the three-glider switch engine
recipe discovered by Luka Okanishi on 12 March 2017.
switch engine channel
Two lines of boats (or other suitable
objects, such as tub with tails) arranged so that a switch engine
can travel between them, in the following manner:

David Bell used this in June 2005 to construct a "bobsled"
oscillator, in which a switch engine factory sends switch engines
down a channel, at the other end of which they are deleted.
switch-engine ping-pong
210515×183739
quadratic growth pattern found by Michael Simkin in October 2014.
Currently this is the smallest starting population (23 cells) known
to result in a quadratic population growth rate. Previous
record-holders include Jaws, mosquito1, mosquito2, mosquito3,
mosquito4, mosquito5, teeth, catacryst, metacatacryst,
Gotts dots, wedge, 26-cell quadratic growth,
25-cell quadratic growth, and 24-cell quadratic growth.
symmetric
Any object which can be rotated and/or flipped over an axis
and still maintain the same shape. Many common small objects such as
the block, beehive, pond, loaf, clock, and blinker are
symmetric. Some larger symmetric objects are Kok's galaxy,
Achim's p16, cross, Eureka, and the pulsar.
Large symmetric objects can easily be created by placing multiple
copies of any finite object together in a symmetrical way. Unless
the individual objects interact significantly, this is considered
trivial and is not considered further here (e.g., two LWSSs
travelling together a hundred cells apart).
There are two kinds of symmetry. Odd symmetry occurs when an
object's line of reflection passes through the center of a line of
cells. Objects with odd symmetry have an odd number of columns or
rows, and can have a gutter. Even symmetry occurs when the line of
reflection follows the boundary between two lines of cells. Objects
with even symmetry have an even number of columns or rows.
Because the Life universe and its rules are symmetric, all
symmetric objects must remain symmetric throughout their evolution.
Most non-symmetric objects keep their non-symmetry as they evolve,
but some can become symmetric, especially if they result in a single
object. Here is a slightly more complicated example where two
gliders interact to form a blockade:
Many useful objects are symmetric along an orthogonal axis. This
commonly occurs by placing two copies of an object side by side to
change the behaviour of the objects due to the inhibition or killing
of new cells at their gutter interface. Examples of this are
twin bees shuttle, centinal, and the object shown in puffer.
Other useful symmetric objects are created by perturbing a symmetric
object using nearby oscillators or spaceships in a symmetric
manner. Examples of this are Schick engine, blinker ship, and
hivenudger.
Many spaceships found by search programs are symmetric because
the search space for such objects is much smaller than for
non-symmetrical spaceships. Examples include dart, 60P5H2V0, and
119P4H1V0.
syringe
A small stable converter found by Tanner Jacobi in March
2015, accepting a glider as input and producing an output Herschel
As of June 2018 it is the smallest known converter of this type, so
it is very often used to handle input gliders in complex signal
circuitry, as described in Herschel circuit. A second glider can
safely follow the first any time after 78 ticks, but overclocking
also allows the syringe to work at a repeat time of 74 or 75 ticks.
If followed by a dependent conduit a simple eater2 can be used
instead of the large welded catalyst shown here. A
ghost Herschel marks the output location.
A different version of the large catalyst, with better clearance
for some situations, can be seen in the switch entry.
table on table
p1

tagalong
An object which is not a spaceship in its own right, but
which can be attached to one or more spaceships to form a larger
spaceship. For examples see Canada goose, fly, pushalong,
sidecar and sparky. See also Schick engine, which consists of
a tagalong attached to two LWSS (or similar).
The following c/4 spaceship (Nicolay Beluchenko, February 2004)
has two wings, either of which can be considered as a tagalong. But
if either wing is removed, then the remaining wing becomes an
essential component of the spaceship, and so is no longer a tagalong.
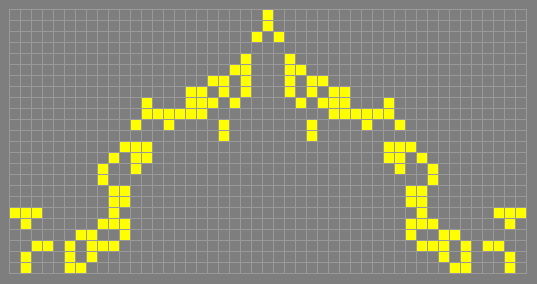
tail spark
A spark at the back of a spaceship. For example, the
1-bit spark at the back of a LWSS, MWSS or HWSS in their less
dense phases.
tame
To perturb a dirty reaction using other patterns so as to
make it clean and hopefully useful. Or to make a reaction work
which would otherwise fail due to unwanted products which interfere
with the reaction.
tandem glider
Two gliders travelling on parallel lanes at a fixed
spacetime offset, usually as a single signal in a
Herschel transceiver. See also glider pair.
Tanner's p46
p46
An oscillator found by Tanner Jacobi on 20
October 2017. This oscillator hassles an evolving pi-heptomino to
produce an phi spark. The spark is very accessible and is able
to perturb many things.

The snakes can be replaced with eaters to form a slightly smaller
version, as shown in the p46 MWSS gun in gliderless
The period of this new oscillator is the same as the old
twin bees shuttle, and so this is able to expand the known p46
technology. For example, a p46 glider gun can be made from a
Tanner's p46 and just one of the twin bees shuttles.
Acting on their own, two copies of Tanner's p46 placed at right
angles to each other with their sparks interacting can produce two
different p46 glider guns and a gliderless p46 MWSS gun. See
p46 gun and gliderless for two of these. These are the first p46
guns found which do not use a twin bees shuttle at all.
teardrop
The following induction coil, or the formation of two
beehives that it evolves into after 20 generations. (Compare
butterfly, where the beehives are five cells further apart.)

technician
p5
Found by Dave Buckingham, January 1973.

technology
The collective set of known reactions exploiting one
subset of the Life universe. Examples of these subsets include
glider synthesis, period 30 glider streams, c/3 spaceships,
sparkers, Herschel conduits, and slow salvos. As new reactions
and objects are found, over time any particular technology becomes
more versatile and complete. Many Life experts like to concentrate
on particular technologies.
tee
A head-on collision between three gliders, producing a
perpendicular output glider that can be used to construct closely
spaced glider salvos, or to inject a glider into an existing
stream. There are several workable recipes. One of the more
useful is the following, because the tandem glider can be generated
by a small Herschel converter, SW1T43:

teeth
A 65-cell quadratic growth pattern found by Nick Gotts in March
2000. This (and a related 65-cell pattern which Gotts found at about
the same time) beat the record previously held by mosquito5 for
smallest population known to have superlinear growth, but was later
superseded by catacryst. See switch-engine ping-pong for the
lowest-population superlinear growth pattern as of July 2018, along
with a list of the record-holders.
telegraph
A pattern created by Jason Summers in February 2003. It
transmits and receives information using a rare type of
reburnable fuse, a lightspeed wire made from a chain of beehives,
at the rate of 1440 ticks per bit. The rate of travel of signals
through the entire transceiver device can be increased to any speed
strictly less than the speed of light by increasing the length of
the beehive chain appropriately.
"Telegraph" may also refer to any device that sends and receives
lightspeed signals; see also p1 telegraph,
high-bandwidth telegraph.
ternary reaction
Any reaction between three objects. In particular,
a reaction in which two gliders from one stream and one glider from a
crossing stream of the same period annihilate each other. This can
be used to combine two glider guns of the same period to produce a
new glider gun with double the period.
test tube baby
p2

tetromino
Any 4-cell polyomino. There are five such objects, shown
below. The first is the block, the second is the T-tetromino and
the remaining three rapidly evolve into beehives.

The Online Life-Like CA Soup Search
A distributed search effort set
up by Nathaniel Johnston in 2009, using a Python script running in
Golly. Results included a collection of the longest-lived 20×20
soups, as well as a census of over 174 billion ash objects. It
has since been superseded by Catagolue.
The Recursive Universe
A popular science book by William Poundstone
(1985) dealing with the nature of the universe, illuminated by
parallels with the game of Life. This book brought to a wider
audience many of the results that first appeared in LifeLine. It
also outlines the proof of the existence of a universal constructor
in Life first given in Winning Ways.
thumb
A spark-like protrusion which flicks out in a manner
resembling a thumb being flicked. Below on the left is a p9 thumb
sparker found by Dean Hickerson in October 1998. On the right is a
p4 example found by David Eppstein in June 2000.

thunderbird
stabilizes at time 243

time bomb
The following pattern by Doug Petrie, which is really just
a glider-producing switch engine in disguise. See
infinite growth for some better examples of a similar nature.
titanic toroidal traveler
The superstring with the following
repeating segment. The front part becomes p16, but the eventual fate
of the detached back part is unknown.

T-nosed p4
p4
Found by Robert Wainwright in October 1989. See also
filter.

T-nosed p5
p5
Found by Nicolay Beluchenko in April 2005.

T-nosed p6
p6
Found by Achim Flammenkamp in September 1994. There
is also a much larger and fully symmetric version found by
Flammenkamp in August 1994.

toad
p2
Found by Simon Norton, May 1970. This is the second most
common oscillator, although blinkers are more than a hundred
times as frequent. See also killer toads. A toad can be used as a
90-degree one-time turner.

The protruding cells at the edges can perturb some reactions by
encouraging and then suppressing births on successive ticks. For
example, a toad can replace the northwest eater in the
Callahan G-to-H converter, allowing it to be packed one diagonal
cell closer to other circuits.
toad-flipper
A toad hassler that works in the manner of the
following example. Two domino sparkers, here pentadecathlons,
apply their sparks to the toad in order to flip it over. When the
sparks are applied again it is flipped back. Either or both domino
sparkers can be moved down two spaces from the position shown and the
toad-flipper will still work, but because of symmetry there are
really only two different types. Compare toad-sucker.

toad-sucker
A toad hassler that works in the manner of the
following example. Two domino sparkers, here pentadecathlons,
apply their sparks to the toad in order to shift it. When the
sparks are applied again it is shifted back. Either or both domino
sparkers can be moved down two spaces from the position shown and the
toad-sucker will still work, but because of symmetry there are really
only three different types. Compare toad-flipper.
toaster
p5
Found by Dean Hickerson, April 1992.

toggleable gun
Any gun that can be turned off or turned on by the
same external signal - the simplest possible switching mechanism. An
input signal causes the gun to stop producing gliders. Another input
signal from the same source restores the gun to its original
function. Compare switchable gun.
Here's a small example by Dean Hickerson from September 1996:
...............O..O....b.........
.OOOO..............O..b..........
O...O..........O...O..bbb........
....O...........OOOO.............
O..O........................aaa..
............................a....
.............................a...
In the figure above, glider B and an LWSS are about to send a glider
NW. Glider A will delete the next glider after B, turning off the
output stream. But if the device were already off, B wouldn't be
present and A would instead delete the leading LWSS, turning the
device back on.
toggle circuit
Any signal-processing circuit that switches back and
forth between two possible states or outputs. An early example is
the boat-bit. More recent discoveries include the semi-Snarks,
which alternate between reflecting and absorbing input gliders.
The following B-to-G converter sends alternate glider outputs in
opposite directions.

toolkit
A set of Life reactions and mechanisms that can be used to
solve any problem in a specific pre-defined class of problems:
glider timing adjustment, salvo creation, seed construction,
etc. See also universal toolkit, technology.
torus
As applies to Life, usually means a finite Life universe which
takes the form of an m × n rectangle with the bottom edge considered
to be joined to the top edge and the left edge joined to the right
edge, so that the universe is topologically a torus. There are also
other less obvious ways of obtaining a toroidal universe.
See also Klein bottle. Every object in a torus universe
obviously either dies or becomes a still life or oscillator.
total aperiodic
Any finite pattern which evolves in such a way that
no cell in the Life plane is eventually periodic. The first example
was found by Bill Gosper in November 1997. A few days later he found
the following much smaller example consisting of three copies of a
p12 backrake by Dave Buckingham.

track
A path made out of conduits, often ending where it begins so
that the active signal object is cycled forever, forming an
oscillator or a gun.
This term has also been used to refer to the lane on which a
glider or spaceship travels. The concept is very similar, but a
reference to a "track" now usually implies a non-trivial supporting
conduit.
tractor beam
A stream of spaceships that can draw an object towards
the source of the stream. The example below shows a tractor beam
pulling a loaf; this was used by Dean Hickerson to construct a
sawtooth.

traffic circle
p100

traffic jam
Any traffic light hassler, such as traffic circle.
The term is also applied to the following reaction, used in most
traffic light hasslers, in which two traffic lights interact in such
a way as to reappear after 25 generations with an extra 6 spaces
between them. See traffic lights extruder for a way to make this
reaction extensible.
traffic light
p2
A common formation of four blinkers.

traffic lights extruder
A growing pattern constructed by Jason
Summers in October 2006, which slowly creates an outward-growing
chain of traffic lights. The growth occurs in waves which travel
through the chain from one end to the other. It can be thought of as
a complex fencepost for a wick that does not need a
wickstretcher.
The following illustrates the reaction used, in which a newly
created traffic light at the left eventually pushes the rightmost one
slightly to the right.
trans-beacon on table
p2

trans-boat with tail
p1

trans-loaf with tail
p1

transparent
In signal circuitry, a term used for a catalyst that is
completely destroyed by the passing signal, then rebuilt. Often
(though not always) the active reaction passes directly through the
area occupied by the transparent catalyst, then rebuilds the catalyst
behind itself, as in the transparent block reaction. See also
transparent lane.
transparent block reaction
A certain reaction between a block and a
Herschel predecessor in which the block reappears in its original
place some time later, the reaction having effectively passed through
it. This reaction was found by Dave Buckingham in 1988. It has been
used in some Herschel conduits, and in the gunstars. Because the
reaction involves a Herschel predecessor rather than an actual
Herschel, the following diagram shows instead a B-heptomino (which
by itself would evolve into a block and a Herschel).

transparent debris effect
A mechanism where a Herschel or other
active reaction completely destroys a catalyst in a particular
location in a conduit. After passing through or past that
location, the same reaction then recreates the catalyst in exactly
its original position. This type of catalysis is surprisingly common
in signal circuitry. For an example, see
transparent block reaction.
The transparent object is most often a very common still life
such as a block or beehive. Rarer objects are not unknown; for
example, a transparent loaf was found by Stephen Silver in October
1997, in a very useful elementary conduit making up part of a
Herschel receiver. However, not surprisingly, rarer objects are
much less likely to reappear in exactly the correct location and
orientation, so transparent reactions involving them are much more
difficult to find, on average.
transparent lane
A path through a signal-producing circuit that can
be used to merge signal streams. The signal is usually a
standard spaceship such as a glider. It can either be produced
by the circuit, or it can come from elsewhere, passing safely through
on the same lane without interacting with the circuit. A good
example is the NW31 converter, which has two glider outputs on
transparent lanes:

The optional third output shown in NW31 is non-transparent,
because the upper eater1 catalyst would get in the way of a passing
glider on the same lane.
trice tongs
p3
Found by Robert Wainwright, February 1982. In terms
of its 7×7 bounding box this ties with jam as the smallest p3
oscillator.

trigger
A signal, usually a single glider, that collides with a
seed constellation to produce a relatively rare still life or
oscillator, or an output spaceship or other signal. The
constellation is destroyed or damaged in the process; compare
circuit, reflector. Here a pair of trigger gliders strike a
dirty seed constellation assembled by Chris Cain in March 2015, to
launch a three-engine Cordership:

"Trigger" is also used when a spaceship reacts with another object
to cause a reaction to occur whenever desired (but perhaps only at
particular intervals). The object being triggered lies dormant
until the reaction is required. All turners and freeze-dried
constellations are triggerable.
In some cases the object is not destroyed so that the reaction can
be repeated after some repeat time. See for example converter
and reflector, and more specifically MWSS out of the blue and
queen bee shuttle pair.
triomino
Either of the two 3-cell polyominoes. The term is rarely
used in Life, since the two objects in question are simply the
blinker and the pre-block.
triple pseudo
The following pattern, found by Gabriel Nivasch in July
2001. It is unique among 32-bit still lifes in that it can be
broken down into three stable pieces but not into two. The term
may also refer to any larger stable pattern with the same property.
See also quad pseudo.

triplet
Any 3-cell polyplet. There are 5 such objects, shown
below. The first two are the two triominoes, and the other three
vanish in two generations.

tritoad
p3
Found by Dave Buckingham, October 1977.

trivial
A trivial period-N oscillator is one in which every cell
oscillates at some smaller factor of N. See omniperiodic. For
example, the joining of a period 3 and a period 4 oscillator as
shown below creates a single object which is a trivial oscillator of
period 12.
.png)
However, there are trivial oscillators that meet this requirement,
but may still be considered to be non-trivial because the
different-period rotors are not separated by stator cells. An
example is Dean Hickerson's trivial p6. Conversely, there are
oscillators formed by trivial combinations of high-period guns or
sparkers that are only technically non-trivial, because the
lower-period components overlap but do not interact in any way.
"Trivial" is also used to describe a parent of an object which
has groups of cells that can be removed without changing the result,
such as isolated faraway cells. For example, here is a trivial
parent of a block.
.png)
trivial p6
p6
An oscillator found by Dean Hickerson in December
1994. Every cell has period less than 6, so this is a trivial
oscillator. It is unusual because it has period-2 cells in contact
with period-3 cells.

trombone slide
An arrangement of four 90-degree reflectors that can
be placed into the path of a glider so as to delay it by an
adjustable number of generations, without changing its lane. More
generally, any combination of circuits may be referred to as a
trombone slide, if the grouping can be moved as a single unit that
functions as a 180-degree glider reflector.
The smallest known trombone slides are made using Snarks. In the
trombone slide shown below, sample input and output gliders are
shown. The input glider will reach the same output location 128
generations sooner if the trombone slide is removed.
If the top and left Snarks are moved together diagonally to the
upper left by N cells, then the glider delay is increased by 8N
generations since the glider has to travel N more cells in each
direction. This sliding action gives the trombone slide its name.
If only the final Snark is moved, then the output glider's path can
be altered by a number of full diagonals.

Trombone slides made of the same type of component cannot alter the
glider path by half-diagonals, and can only change the timing by
multiples of 8 generations. For other timing changes, different
components are necessary. These may be stable like the
Silver reflector or the colour-changing example shown in the
reflector article, or periodic like the various bumpers.
true
Opposite of pseudo. A gun emitting a period n stream of
spaceships (or rakes) is said to be a true period n gun if its
mechanism oscillates with period n. The same distinction between
true and pseudo also exists for puffers. An easy way to check that
a gun is true period n is to stop the output with an eater, and
check that the result is a period-n oscillator.
True period n guns are known to exist for all periods greater than
61 (see My Experience with B-heptominos in Oscillators), but only a
few smaller periods have been achieved, namely 20, 22, 24, 30, 36,
40, 44, 45, 46, 48, 50, and 54 through 61. See also Quetzal for
the 54-61 range.
------------------------------------
Period Discoverers Date
------------------------------------
20 Matthias Merzenich May 2013
Noam Elkies
22 David Eppstein Aug 2000
Jason Summers
24 Noam Elkies Jun 1997
30 Bill Gosper Nov 1970
36 Jason Summers Jul 2004
40 Adam P. Goucher Mar 2013
Matthias Merzenich
Jason Summers
44 Dave Buckingham Apr 1992
45 Matthias Merzenich Apr 2010
46 Bill Gosper 1971
48 Noam Elkies Jun 1997
50 Dean Hickerson Oct 1996
Noam Elkies
Dave Buckingham
54 Dieter Leithner Jan 1998
Noam Elkies
Dave Buckingham
55 Stephen Silver Oct 1998
56 Dieter Leithner Jan 1998
Dave Buckingham
Noam Elkies
57 Matthias Merzenich Apr 2016
58 'thunk' Apr 2016
Matthias Merzenich
Chris Cain
59 Adam P. Goucher Dec 2009
Jason Summers
60 Bill Gosper Nov 1970
61 Luka Okanishi Apr 2016
------------------------------------
tub
p1

tubber
p3
Found by Robert Wainwright before June 1972.

tubeater
A pattern that consumes the output of a tubstretcher. The
smallest known tubeater was found by Nicolay Beluchenko (September
2005), and is shown below in conjunction with the smallest known
tubstretcher.

tubstretcher
Any wickstretcher in which the wick is two diagonal
lines of cells forming, successively, a tub, a barge, a
long barge, etc. The first one was found by Hartmut Holzwart in
June 1993, although at the time this was considered to be a
boatstretcher (as it was shown with an extra cell, making the tub
into a boat). The following small example is by Nicolay Beluchenko
(August 2005), using a quarter.

In October 2005, David Bell constructed an adjustable high-period
diagonal c/4 rake that burns tubstretcher wicks to create
gliders, which are then turned and duplicated by convoys of
diagonal c/4 spaceships to re-ignite the stabilized ends of the
same wicks.
tub with tail
p1
The following 8-cell still life. See eater
for a use of this object.

tumbler
p14
The smallest known p14 oscillator. Found by George
Collins in 1970. The oscillator generates domino sparks, but
they are fragile and no use has been found for them to date. In each
domino, one cell is "held" (remains alive) for two generations, the
other for three. By contrast, useful domino sparks are usually alive
for only one tick per oscillator period.

turner
A one-time glider reflector, or in other words a
single-glider seed (the term is seldom or never used in relation to
spaceships other than gliders). One-time turners may be 90-degree or
180-degree, or they may be 0-degree with the output in the same
direction as the input. A reusable turner would instead be called a
reflector. Shown on the top row below are the four 90-degree turner
reactions that use common small ash objects: boat, eater1,
long boat, and toad.

Of the reactions on the first row, the glider output is the same
parity for all but the long boat. The three still lifes are all
colour-changing, but the toad happens to be a colour-preserving
turner. The third row shows an aircraft carrier serving as a
"0-degree turner" that is also colour-changing.
Three of the simplest 180-degree turners are shown in the second
row. The Blockic 180-degree turner is colour-preserving. The
long boat and long ship are again colour-changing; this is
somewhat counterintuitive as the output glider is on exactly the same
lane as the input glider, but gliders travelling in opposite
directions on the same lane always have opposite colours.
Many small one-time turner constellations have also been
catalogued. The 90-degree two-block turner on the right, directly
below the toad, is also colour-changing but has the opposite parity.
A one-time turner reaction can be used as part of a glider
injection mechanism, or as a switching mechanism for a signal.
If a previous reaction has created the sacrificial object, then a
later glider is turned onto a new path. Otherwise it passes through
the area unaffected. This is one way to create simple switching
systems or logic circuits. An example is shown in demultiplexer.
turning toads
p4 wick
Found by Dean Hickerson, October 1989.

turtle
c/3 orthogonally, p3
A spaceship found by Dean Hickerson
in August 1989 that produces a domino spark at the back.
Hickerson used this spark to convert an approaching HWSS into a
loaf, as part of the first sawtooth. (Also see tractor beam).
The shape of the back end of the turtle is distinctive. Very similar
but wider back ends have been found in other c/3 ships to produce
period 9 and 15 spaceships.

twin bees shuttle
p46
Found by Bill Gosper in 1971, this was the
basis of all known true p46 guns, and all known p46 oscillators
except for glider signal loops using Snarks, until the
discovery of Tanner's p46 in 2017. See new gun for an example.
There are numerous ways to stabilize the ends, two of which are shown
in the diagram. On the left is David Bell's double block reaction
(which results in a shorter, but wider, shuttle than usual), and on
the right is the stabilization by a single block. This latter method
produces the very large twin bees shuttle spark which is useful in
a number of ways. See metamorphosis for an example. Adding a
symmetrically placed block below this one suppresses the spark. See
also p54 shuttle.

twin bees shuttle pair
Any arrangement of two twin bees shuttles
such that they interact. There are many ways that the two shuttles
can be placed, either head-to-head, or else at right angles. Glider
guns can be constructed in at least five different ways. Here is one
by Bill Gosper in which the shuttles interact head-to-head:

For other examples, see new gun, edge shooter, double-barrelled
and natural Heisenburp.
twin bees shuttle spark
The large and distinctive long-lived spark
produced, most commonly, by the twin bees shuttle. It starts off
as shown below.
.png)
After 3 generations it becomes symmetric along the horizontal axis,
after 9 generations it becomes symmetric along the vertical axis
also, and finally dies after 18 generations.
Since the spark is isolated and long-lived, there are many possible
perturbations that it can perform. One of the most useful is
demonstrated in metamorphosis where a glider is converted into a
LWSS. Another useful one can turn a LWSS by 90 degrees:
.png)
two-arm
The type of universal constructor exemplified by the
original Gemini spaceship, where two independently programmed
construction arms sent gliders in pairs on 90-degree paths to
collide with each other at the construction site. Construction
recipes for two-arm constructors are much more efficient in general,
but they require many more circuits and multiple independent data
streams, which both tend to increase the complexity of
self-constructing circuitry. Compare single-arm.
two eaters
p3
Found by Bill Gosper, September 1971.

two pulsar quadrants
p3
Found by Dave Buckingham, July 1973.
Compare pulsar quadrant.

unit Life cell
A rectangular pattern, of size greater than 1×1, that
can simulate Life in the following sense. The pattern by itself
represents a dead Life cell, and some other pattern represents a live
Life cell. When the plane is tiled by these two patterns (which then
represent the state of a whole Life universe) they evolve, after a
fixed amount of time, into another tiling of the plane by the same
two patterns which correctly represents the Life generation following
the one they initially represented.
It is usual to use the prefix "meta-" for simulated Life features,
so, for example, for the first known unit Life cell (constructed by
David Bell in January 1996), one metatick is 5760 ticks, and one
metacell is 500×500 cells. Capital letters were originally used to
make this distinction - e.g., Generation, Cell - but this usage is no
longer common.
In December 2005, Jason Summers constructed an analogous unit cell
for Wolfram's Rule 110, a one-dimensional cellular automaton that
is known be universal. See also OTCA metapixel, p1 megacell.
universal computer
A computer that can compute anything that is
computable. (The concept of computability can be defined in terms of
Turing machines, or by Church's lambda calculus, or by a number of
other methods, all of which can be shown to lead to equivalent
definitions.) The relevance of this to Life is that both Bill Gosper
and John Conway proved early on that it is possible to construct a
universal computer in the Life universe. (To prove the universality
of a cellular automaton with simple rules was in fact Conway's aim
in Life right from the start.) Conway's proof is outlined in
Winning Ways, and also in The Recursive Universe.
Until recently, no universal Life computer had ever been built in
practice In April 2000, Paul Rendell completed a Turing machine
construction (see http://rendell-attic.org/gol/tm.htm for details).
This, however, has a finite tape, as opposed to the infinite tape of
a true Turing machine, and is therefore not a universal computer.
But in November 2002, Paul Chapman announced the construction of a
universal computer, see
http://www.igblan.free-online.co.uk/igblan/ca/. This is a universal
register machine based around Dean Hickerson's
sliding block memory.
In 2009 Adam P. Goucher constructed a programmable Spartan
universal computer/constructor pattern using stable Herschel
circuitry. It included memory tapes and registers capable of holding
a simple universal instruction set and program data, and also a
minimal single-arm universal constructor. Its size meant that it
was extremely impractical to program it to be self-constructing,
though this was theoretically possible if the escape of large numbers
of gliders could be allowed as a side effect.
In February 2010, Paul Rendell completed a universal Turing machine
design with an unlimited tape, as described in his thesis at
http://eprints.uwe.ac.uk/22323/1/thesis.pdf.
In 2016 Nicolas Loizeau ("Coban") completed a Life pattern
emulating a complete 8-bit programmable computer.
See also universal constructor.
universal constructor
A pattern that is capable of constructing
almost any pattern that has a glider synthesis. This definition is
a bit vague. A precise definition seems impossible because it is not
known, for example, whether all still lifes are constructible. In
any case, a universal constructor ought to be able to construct
itself in order to qualify as such.
An outline of Conway's proof that such a pattern exists can be
found in Winning Ways, and also in The Recursive Universe. The
key mechanism for the production of gliders with any given path and
timing is known as side-tracking, and is based on the
kickback reaction. A universal constructor designed in this way
can also function as a universal destructor: it can delete almost
any pattern that can be deleted by gliders.
In May 2004, Paul Chapman and Dave Greene produced a prototype
programmable universal constructor. This is able to construct
objects by means of slow glider constructions. It likely that it
could be programmed to construct itself, but the necessary program
would be very large; moreover an additional mechanism would be needed
in order to copy the program.
A universal constructor is theoretically most useful when attached
to a universal computer, which can be programmed to control the
constructor to produce the desired pattern of gliders. In what
follows I will assume that a universal constructor always includes
this computer.
The existence of a universal constructor/destructor has a number of
theoretical consequences.
For example, the constructor could be programmed to make copies of
itself. This is a replicator.
The constructor could even be programmed to make just one copy of
itself translated by a certain amount and then delete itself. This
would be a (very large, very high period) spaceship. Any
translation is possible, so that the spaceship could travel in any
direction. If the constructor makes a rotated but unreflected copy
of itself, the result would be a looping spaceship or
reflectorless rotating oscillator.
The constructor could also travel slower than any given speed,
since we could program it to perform some time-wasting task (such as
repeatedly constructing and deleting a block) before copying itself.
Of course, we could also choose for it to leave some debris behind,
thus making a puffer.
It is also possible to show that the existence of a universal
constructor implies the existence of a stable reflector. This
proof is not so easy, however, and is no longer of much significance
now that explicit examples of such reflectors are known.
Progressively smaller universal-constructor mechanisms without an
attached universal computer have been used in the
linear propagator, spiral growth pattern, and the Demonoids and
Orthogonoid. See also single-channel.
Another strange consequence of the existence of universal
constructors was pointed out by Adam P. Goucher and Tanner Jacobi in
2015. Any glider-constructible pattern, no matter how large, can be
constructed with a fixed number of gliders, by working out a
construction recipe for a universal constructor attached to a decoder
that measures the distance to a faraway object. The object's
position encodes a numeric value that can be processed to retrieve as
many bits of information as are needed to build a slow salvo to
construct any given target pattern. The simplest design, requiring
less than a hundred gliders, is described in reverse caber tosser.
universal register machine
= URM
universal regulator
A regulator in which the incoming gliders are
aligned to period 1, that is, they have arbitrary timing (subject to
some minimum time required for the regulator to recover from the
previous glider).
Paul Chapman constructed the first universal regulator in March
2003. It is adjustable, so that the output can be aligned to any
desired period. A stable universal regulator was constructed by
Dave Greene in September 2015, with a minimum delay between test
signals of 1177 ticks. Later stable versions have reduced the delay
to 952 ticks.
A universal regulator can allow two complex circuits to interact
safely, even if they have different base periods. For example,
signals from a stable logic circuit could be processed by a
period-30 mechanism, though the precise timing of those signals would
change in most cases.
universal toolkit
A set of Life reactions and mechanisms that can be
used to construct any object that can be constructed by glider
collisions. Different universal toolkits were used to construct the
linear propagator, 10hd Demonoid, 0hd Demonoid, and
Orthogonoid, for example.
universe
The topology of the cells in the Life grid. In the normal
universe (the usual Life arena), the grid is infinite in both
directions. In a cylindrical universe, the grid is finite in one
direction, and the cells at the two edges are adjacent to each other.
In a torus universe, the grid is finite in both directions, and the
cells at the top and bottom edges are adjacent, and the cells at the
left and right edges are adjacent. There are several other more
obscure types of universe.
Objects found in the cylindrical and toroidal universes can also
run in the normal universe if an infinite number of copies are
arranged to support each other. Sometimes the objects can be
supported in other ways to make a useful finite object. This is one
reason that soup searches are run in alternative universes, to find
such objects.
unix
p6
Two blocks eating a long barge. This is a useful
sparker, found by Dave Buckingham in February 1976. The name
derives from the fact that it was for some time the mascot of the
Unix lab of the mathematics faculty at the University of Waterloo.

unknown fate
An object whose fate is in some way unanswerable with
our current knowledge. The simplest way that the fate of an object
can be unknown involves the question of whether or not it exhibits
infinite growth. For example, the fate of the
Fermat prime calculator is currently unknown, but its behaviour is
otherwise predictable.
A different type of unknown fate is that of the
Collatz 5N+1 simulator, which may become stable, or an oscillator,
or have an indefinitely growing bounding box. Its behavior is
otherwise predictable, and unlike the Fermat prime calculator the
population is known to be bounded.
Life objects having even worse behaviour (e.g. chaotic growth)
are not known as of July 2018.
U-pentomino
Conway's name for the following pentomino, which
rapidly dies.

URM
A universal register machine, particularly Paul Chapman's Life
implementation of such a machine. See universal computer for more
information.
vacuum
Empty space. That is, space containing only dead cells.
Venetian blinds
The p2 agar obtained by using the pattern O..O to
tile the plane. Period 2 stabilizations of finite patches of this
agar are known.

volatility
in cells
of its rotor divided by the sum of the sizes of its rotor and its
stator. In other words, it is the proportion of cells involved in
the oscillator which actually oscillate. For many periods there are
known oscillators with volatility 1, see for example Achim's p16,
figure-8, Kok's galaxy, mazing, pentadecathlon, phoenix,
relay, smiley and tumbler. Such an oscillator of period 3 was
found in August 2012 by Jason Summers.

The smallest period for which the existence of such statorless
oscillators is undecided is 7. There are oscillators with volatility
arbitrarily close to 1 for all but finitely many periods, because of
the possibility of feeding the gliders from a true period n gun
into an eater.
The term "volatility" is due to Robert Wainwright. See also
strict volatility.
von Neumann neighbourhood
The set of all cells that are orthogonally
adjacent to a cell or group of cells. The von Neumann neighbourhood
of a cell can be thought of as the points at a Manhattan distance of
1 from that cell. Compare Moore neighbourhood.
Cell neighbourhoods can also be defined with a higher range. The
von Neumann neighbourhood of range n can be defined recursively as
the von Neumann neighbourhood of the von Neumann neighbourhood of
range n-1. For example, the von Neumann neighbourhood of range 2 is
the set of all cells that are orthogonally adjacent to the range-1
von Neumann neighbourhood.
Wainwright's tagalong
A small p4 c/4 diagonal tagalong that has 7
cells in every phase. It is shown here attached to the back of a
Canada goose.

washerwoman
2c/3 p18 fuse
A fuse discovered by Earl Abbe,
published in LifeLine Vol 3, September 1971.

washing machine
p2
Found by Robert Wainwright before June 1972.

wasp
c/3 orthogonally, p3
The following spaceship which produces
a domino spark at the back. It is useful for perturbing other
objects. Found by David Bell, March 1998.

waterbear
(23,5)c/79 obliquely, p158
A self-supporting oblique
macro-spaceship constructed by Brett Berger on December 28, 2014.
It is currently the fastest oblique macro-spaceship in Conway's Game
of Life by several orders of magnitude, and is also the smallest
known oblique macro-spaceship in terms of bounding box, superseding
the Parallel HBK. It is no longer the smallest or fastest oblique
spaceship due to the discovery in 2018 of the elementary
knightship Sir Robin.
Previous oblique spaceships, the Gemini and the
half-baked knightships, are stationary throughout almost all of
their life cycles, as they construct the necessary mechanisms to
support a sudden short move. The waterbear constructs support for
reburnable fuse reactions involving (23,5)c/79 Herschel climbers
that are in constant motion.
wave
A wick-like structure attached at both ends to moving
spaceship-like patterns, in such a way that the entire pattern is
mobile. Especially if the wave gets longer over time, the supporting
patterns are wavestretchers.
Also, the gliders or spaceships emitted by a rake may be referred
to as a wave, again because the line as a whole appears to move in a
different direction from the individual components, due to the rake's
movement. Compare with stream.
In general a wave can be interpreted as moving at a variety of
different velocities, depending on which specific subcomponents are
chosen as the starting and ending points for calculating speed and
direction. See antstretcher, wavestretcher for a practical
example of identical wave ends being connected to spaceships with
different velocities.
wavefront
p4
Found by Dave Buckingham, 1976 or earlier.

wavestretcher
A spaceship pattern that supports a connection to an
extensible periodic wick-like structure, whose speed and/or
direction of propagation are different from those of the
wavestretcher spaceship.
Connecting the following to a standard diagonal antstretcher
creates a new oblique wavestretcher (a type of growing spaceship)
and also an alternate space nonfiller mechanism.
A required supporting c/5 spark is shown at the right edge. It can
be supplied by a spider or another c/5 orthogonal spaceship with a
similar edge spark. Alternatively, the c/5 component could
theoretically be replaced by a supporting spaceship travelling
diagonally at c/6, to support the same oblique trail of ants. As of
June 2018 no workable c/6 component has been found.
weekender
2c/7 orthogonally, p7
Found by David Eppstein in January
2000. In April 2000 Stephen Silver found a tagalong for a pair of
weekenders. At present, n weekenders pulling n-1 tagalongs
constitute the only known spaceships of this speed or period,
except for variants of the weekender distaff that suppress its
output gliders.
weekender distaff
2c/7, p16982
The first orthogonal 2c/7 rake,
constructed by Ivan Fomichev on May 22nd, 2014. It uses the weak
sparks from weekenders to perturb an LWSS into an active reaction
in a variable-period loop, which produces a series of slow salvo
gliders that finally rebuilds the LWSS.
weld
To join two or more still lifes or oscillators together.
This is often done in order to fit the objects into a smaller space
than would otherwise be possible. The simplest useful example is
probably the integral sign, which can be considered as a pair of
welded eater1s.
Wheels, Life, and other Mathematical Amusements
One of Martin
Gardner's books (1983) that collects together material from his
column in Scientific American. The last three chapters of this book
contain all the Life stuff.
why not
p2
Found by Dave Buckingham, July 1977.

wick
A stable or oscillating linearly repeating pattern that can be
made to burn at one end. See fuse. Wicks are often fairly
dense, with repeating units directly connected or at least adjacent
to each other, as in the beehive lightspeed wire for example.
However, sparse wicks such as the blocks in the
31c/240 Herschel-pair climber are known, and arbitrarily sparse
wicks can be constructed.
wickstretcher
A spaceship-like object which stretches a wick that
is fixed at the other end. The wick here is assumed to be in some
sense connected, otherwise most puffers would qualify as
wickstretchers. The first example of a wickstretcher was found in
October 1992 (front end by Hartmut Holzwart and back end by Dean
Hickerson) and stretches ants at a speed of c/4. This is shown
below with an improved back end found by Hickerson the following
month.

Diagonally moving c/4 and c/12 wickstretchers have also been built:
see tubstretcher and linestretcher. In July 2000 Jason Summers
constructed a c/2 wickstretcher, stretching a p50 traffic jam wick,
based on an earlier (October 1994) pattern by Hickerson. A c/5
diagonal wickstretcher was found in January 2011 by Matthias
Merzenich, who also discovered a c/5 orthogonal wickstretcher two
years later in March 2013.
wicktrailer
Any extensible tagalong or component that can be
attached to itself, as well as to the back of a spaceship. The
number of generations that it takes for the component to occur again
in the same place is often called the period of the wicktrailer.
This has little relation to the period of the component. See
branching spaceship for an example of a wicktrailer that is part of
a p2 spaceship, but repeats itself in the same location at period 20.
windmill
p4
Found by Dean Hickerson, November 1989.

Winning Ways
1982
by Elwyn Berlekamp, John Conway
and Richard Guy on mathematical games. The last chapter of the
second volume concerns Life, and outlines a proof of the existence of
a universal constructor.
wire
A repeating stable structure, usually fairly dense, that a
signal can travel along without making any permanent change. Known
wires include the diagonal 2c/3 wire, and orthogonal
lightspeed wire made from a chain of beehives. Diagonal lightspeed
wires are known, but the required signals are fairly complex and have
no known glider synthesis.
with the grain
A term used for negative spaceships travelling in
zebra stripes agar, parallel to the stripes, and also for
with-the-grain grey ships.
Below are three small examples of "negative spaceships" found by
Gabriel Nivasch in July 1999, travelling with the grain through a
stabilized finite segment of zebra stripes agar:

It has been proven that signals travelling non-destructively with the
grain through zebra stripes cannot travel at less than the
speed of light.
with-the-grain grey ship
A grey ship in which the region of density
1/2 consists of lines of ON cells lying parallel to the direction in
which the spaceship moves. See also against-the-grain grey ship.
worker bee
p9
Found by Dave Buckingham in 1972. Unlike the similar
snacker this produces no sparks, and so is not very important.
Like the snacker, the worker bee is extensible. It is, in fact, a
finite version of the infinite oscillator which consists of six ON
cells and two OFF cells alternating along a line. Note that Dean
Hickerson's new snacker ends also work here.
*WSS
Any of the standard orthogonal spaceships - LWSS, MWSS, or
HWSS. At one point the term fish was more common for this group
of spaceships.
x66
c/2 orthogonally, p4
Found by Hartmut Holzwart, July 1992. Half
of this can be escorted by an HWSS. The name refers to the fact that
every cell (live or dead) has at most 6 live neighbours (in contrast
to spaceships based on LWSS, MWSS or HWSS). In fact this
spaceship was found by a search with this restriction.

Xlife
A popular freeware Life program that runs under the X Window
System. The main Life code was written by Jon Bennett, and the X
code by Chuck Silvers.
Y-pentomino
Conway's name for the following pentomino, which
rapidly dies.

zone of influence
The set of cells on which a chosen cell or pattern
can potentially exert an influence in a given number of generations
N. If N is not specified it is generally taken to be one, in which
case the zone of influence simply coincides with the Moore
neighbourhood of the cell or pattern.
The set for N generations consists of all the cells to which at
least N paths of length N can be traced from the cell(s) in question.
Contrast this with the range-N Moore neighbourhood, which consists of
all cells to which at least one path of length n can be traced.
Z-pentomino
Conway's name for the following pentomino, which
rapidly dies.

zweiback
p30
An oscillator in which two HW volcanoes hassle a
loaf. This was found by Mark Niemiec in February 1995. A smaller
version using Scot Ellison's reduced HW volcano is shown below.

David I. Bell, Spaceships in Conway's Life.
Series of articles posted on comp.theory.cell-automata,
Aug-Oct 1992. Now available from
his website.
David I. Bell, Speed c/3 Technology in Conway's Life,
17 December 1999. Available from
his website.
Elwyn R. Berlekamp, John H. Conway and Richard K. Guy,
Winning Ways for your Mathematical Plays, II: Games in Particular.
Academic Press, 1982.
David J Buckingham, Some Facts of Life. BYTE, December 1978.
Dave Buckingham, My Experience with B-heptominos in Oscillators.
12 October 1996.
Available
from Paul Callahan's website.
David J. Buckingham and Paul B. Callahan,
Tight Bounds on Periodic Cell Configurations in Life.
Experimental Mathematics 7:3 (1998) 221-241.
Available at
http://tinyurl.com/TightBoundsOnCellConfigs.
Noam D. Elkies, The still-Life density problem and its
generalizations,
pp228-253 of "Voronoi's Impact on Modern Science,
Book I", P. Engel, H. Syta (eds), Institute of Mathematics, Kyiv, 1998
= Vol.21 of Proc. Inst. Math. Nat. Acad. Sci. Ukraine,
math.CO/9905194.
Martin Gardner, Wheels, Life, and other Mathematical Amusements.
W. H. Freeman and Company, 1983.
R. Wm. Gosper, Exploiting Regularities in Large Cellular Spaces.
Physica 10D (1984) 75-80.
N. M. Gotts and P. B. Callahan, Emergent structures in sparse fields of
Conway's 'Game of Life', in Artificial Life VI: Proceedings of the
Sixth International Conference on Artificial Life, MIT Press, 1998.
Mark D Niemiec, Life Algorithms. BYTE, January 1979.
William Poundstone, The Recursive Universe.
William Morrow and Company Inc., 1985.









